If we had to choose one skill as the most important in algebra, it would probably be solving equations.

The best way to view solving equations is as a kind of game.

The goal of the game is to find what number is represented by the letter in the equation (e.g. y = 4).

The rule of the game is that if you do any arithmetical operation on one side of the equation, you must do the exact same arithmetical operation on the other side (e.g. if you subtract 3 from the left you must also subtract 3 from the right. If you add 4x to the left, you must also add 4x to the right).

So we keep doing arithmetic to both sides of the equation until our equation looks like x = …, with the … being our answer.

Worked Examples

• Find x if x + 5 = 7
• Find y if 2y + 1 = 9
• Solve 17 – 2x = 7

Exercise 1

Solve the following equations:

1.) a + 6 = 9

2.) b + 3 = 11

3.) 6 = c+5

4.) 8 + d = 12

5.) 2e + 1 = 11

6.) 3f + 4 = 19

7.) 2 + 5g = 17

8.) h + 7 = 11

9.) 10 = 3i + 1

10.) 10 + 3j = 13

11.) k + 7 = 7

12.) 2l + 1 = 5

13.) 9 = 3 + 2m

14.) 25 – 3n = 10

15.) 6o = 60

16.) p – 1 = 5

17.) 1 = q – 2

18.) 8 = 18 – 5r

19.) 25 = 5s

20.) 10 – 4t = -2

21.) 3u – 1 = 14

22.) 56 = 8v

23.) 3w – 4 = 17

24.) 15 = 4x – 1

25.) 12 = 5y – 8 – y

26.) 5z + 1 + 6z = 122

(Hint for questions 25 and 25: Simplify first)

Inverse Operations

When we solve equations, we are effectively using inverse operations. So if 3 is added to y, we subtract 3 from both sides of our equation to “get rid of it”. If y is divided by 7, we multiply both sides by 7 to “get rid of it”. Thinking like this can help us.

Worked Examples

• Solve:
  • m ÷ 5 = 10
  • t ÷2 + 1 = 5

Exercise 2

1.) x ÷ 3 = 3

2.) p ÷ 4 + 1 = 3

3.) T ÷ 5 – 3 = 2

4.) t ÷ 2 = 2

5.) 12 = g ÷ 11 + 10

6.) 7 = y ÷ 6

7.) 12 = x ÷ 12

8.) 11 – 3y = -1

9.) 20 = -2m

10.) -3x = 15

Word Problems requiring solution of equations

To combine everything that we have learned in Algebra so far, we can now tackle word problems, by rewriting the word problem as and algebraic equation and then solving the equation.

Worked Examples

Dasha and Masha have $20 altogether. Dasha has $6. How much does Masha have?

The perimeter of a rectangular field is 80m. If the length of the field is 30m, then what is its width?

Exercise 3

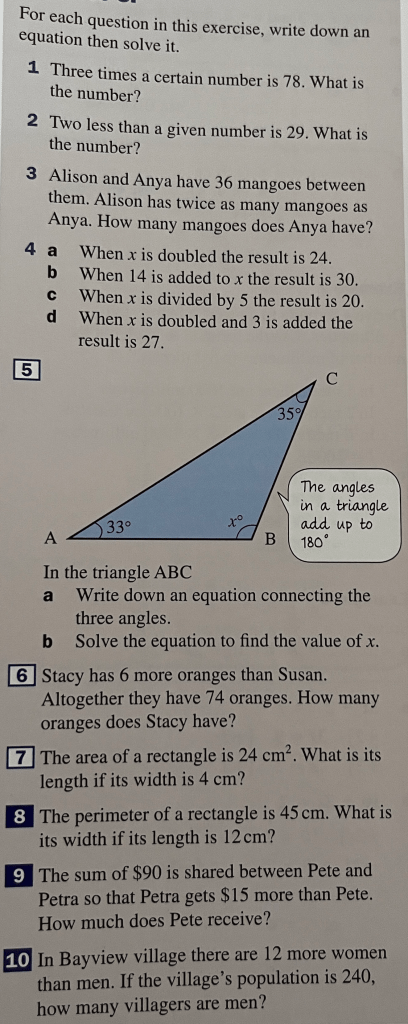
Answers to all three exercises