As well as reflective symmetry, some shapes have rotational symmetry.

Rotational symmetry is when you can rotate a shape around a point and get back to the same shape. If the shape only “gets back to itself” once in a complete term, it has rotational symmetry order 1. If it “gets back to itself” twice then it has rotational symmetry order 2. No shape has rotational symmetry order zero.

Worked Example

What order of symmetry do the following letters have: A, H, I, X ?

Exercise 1

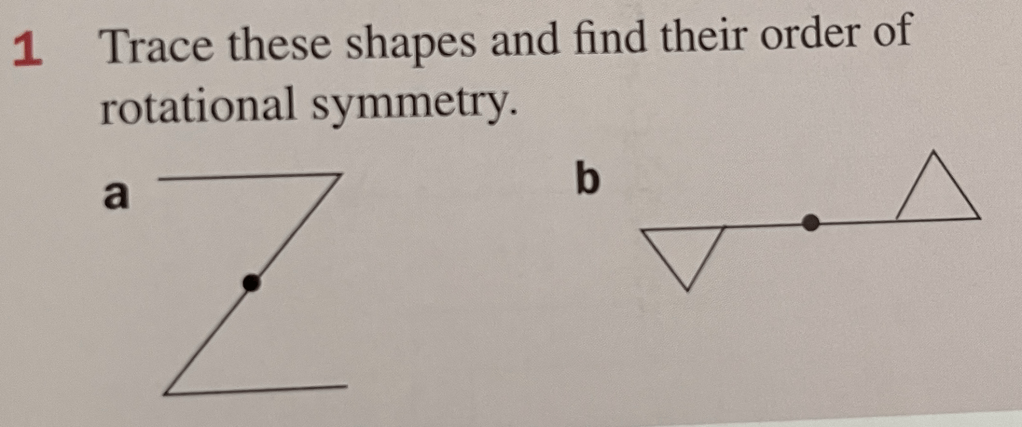
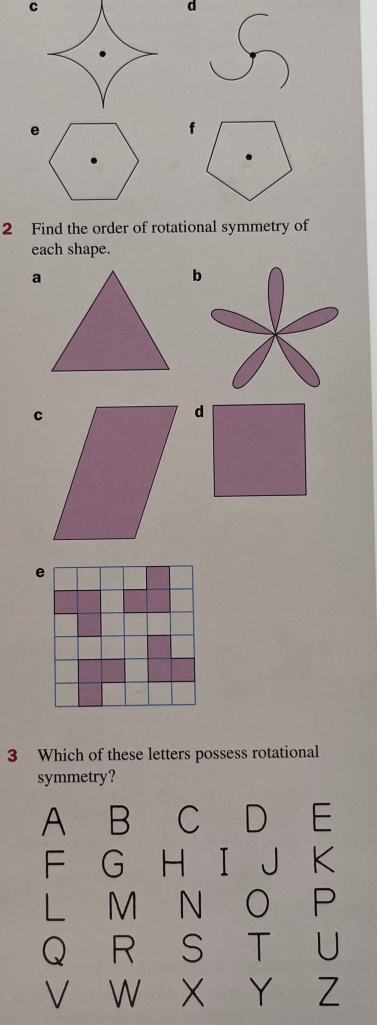
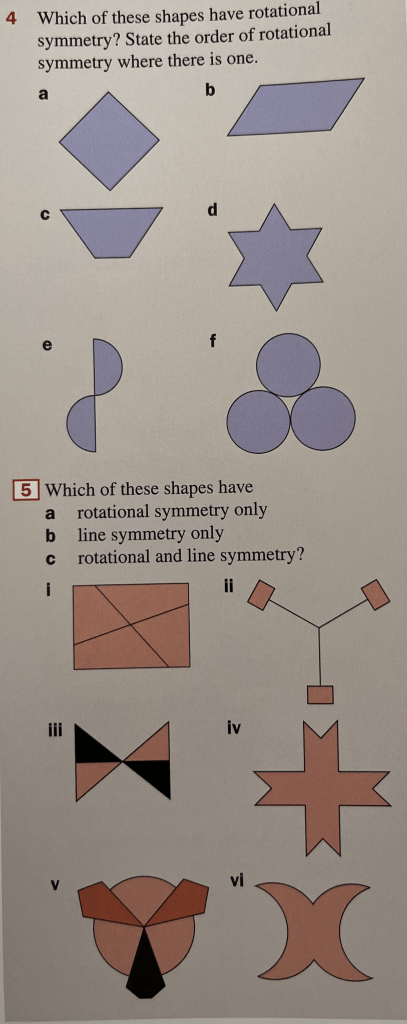
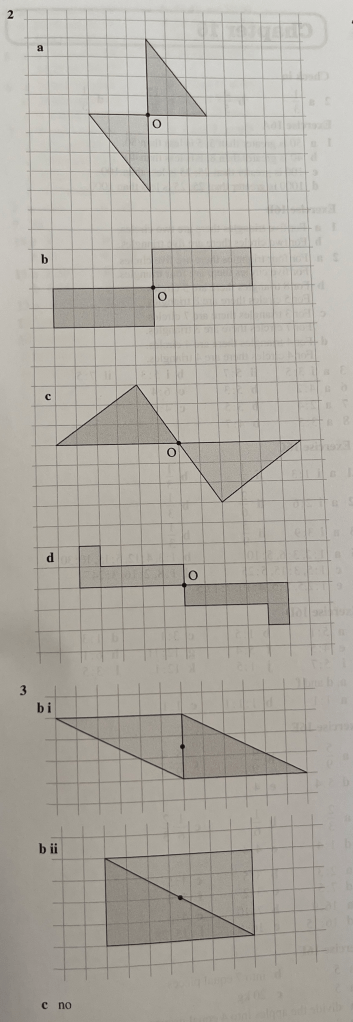
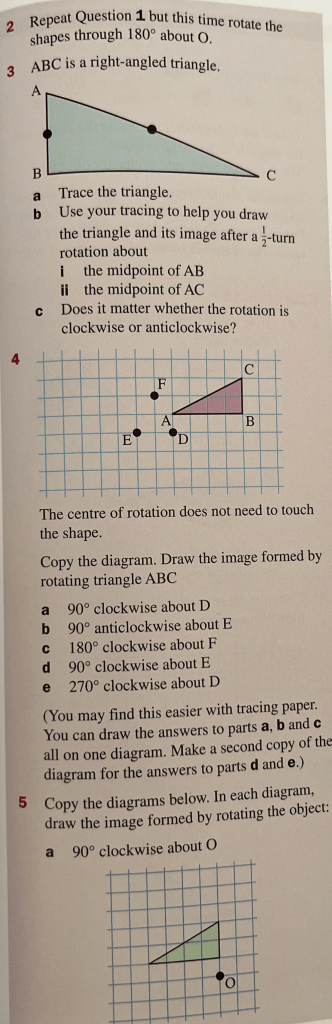
Rotations around a given centre

Just as we could reflect objects through a given mirror line to find their image, we can also rotate objects around a given centre of rotation to find their image. Let’s see some examples from the teacher on the board.

Exercise 2

Answers to both exercises