Numbers like 3, 10, 7 are very nice, but unfortunately, with some subtractions, like 3 – 7, the result is not a positive number like these. Because of this we need negative numbers (these are numbers whose value is less than zero.

These numbers can be confusing, for example because -10 is smaller than -8. Some people like to compare them to temperature or to debt to help them remember how they work.

A very useful tool when working with negative numbers is a number line, especially when you are doing addition or subtraction. It is always okay to draw a number line when you are trying to do a calculation with negative numbers.

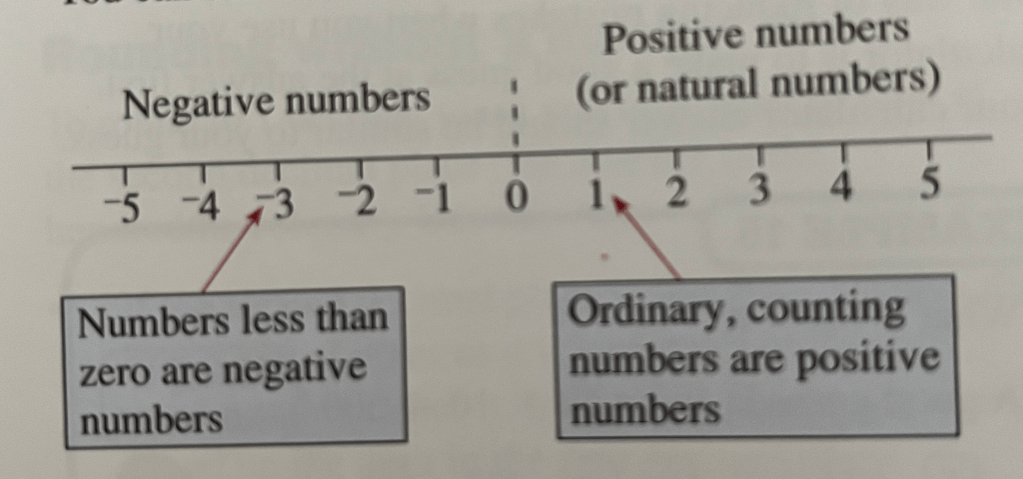
Worked Example

• Which of the following numbers is greater:
  • 2 and -3
  • -2 and -5

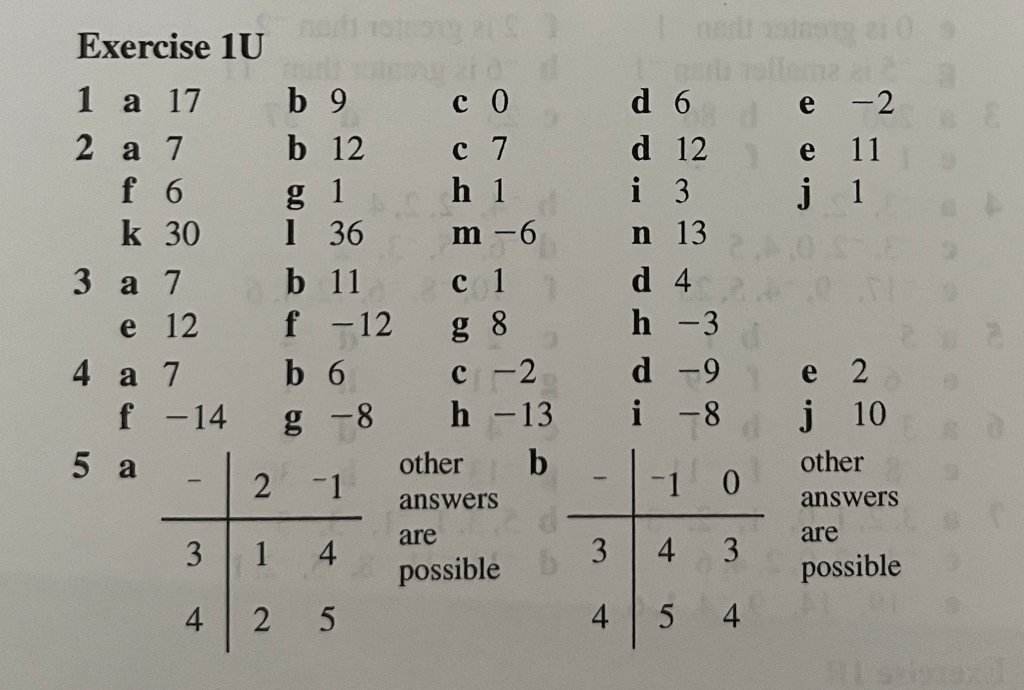
Exercise 1

Using a number line

• Let’s look at using a number line to answer the following questions
  • 6 – 8
  • 2 – 5
  • -1 + 4
  • -2 – 3

Exercise 2

Addition with negative numbers

When we add numbers, the order doesn’t matter, so 3 + 5 is the same as 5 + 3, and also 2 + 9 + 7 is the same as 2 + 7 + 9 or 9 + 2 + 7 or 9 + 7 + 2. This can help us when we are dealing with negative numbers so if we have 4 and want to add -3, instead of thinking of this as 4 + -3 we can think of it as -3 + 4 and use a number line to calculate it.

Exercise 3

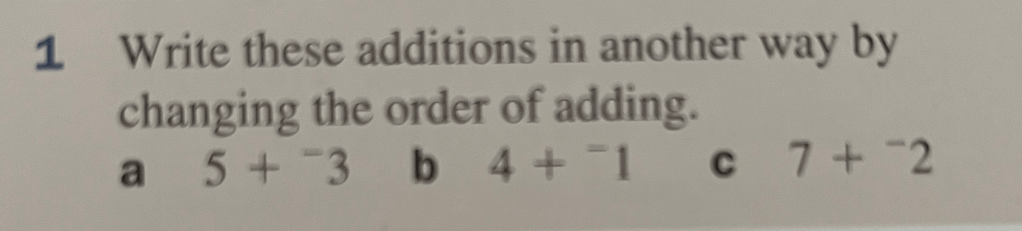
We can also use number lines to add negative numbers. We do this by noticing that -2 + -3 is the same as -2 -3 (think of the temperature comparison. If a drink is at -2 degrees and you add and ice cube at -3 degrees you can bring its temperature down to -5 degrees. So it’s like adding cold makes things colder.

Exercise 4

Subtracting negative numbers

Following our metaphor above, we can think of subtracting negative numbers as like removing ice cubes from a drink -> taking away a negative is the same as adding the equivalent positive. So 3 – -2 is actually 5.

Another way to see this is to consider the following pattern:

• 3 – 2 = 1
• 3 – 1 = 2
• 3 – 0 = 3
• 3 – -1 = ?

It doesn’t matter what way you remember it, as long as you remember that subtracting a negative number is equivalent to adding a positive number with the same absolute value.

Worked Example

• Calculate
  • -6 – -3
  • -4 – -2
  • -6 – -3 + 4
  • -7 + -5 – -4

Exercise 5

Final comments

Negative numbers appear a lot in real life. Some common examples are with temperature, with money, or with height when we consider somebody diving or digging underground. For our last two exercises, first we have and exercise looking at practical questions involving a negative numbers, and then a mixed exercise to practice everything we’ve learned about negative numbers.

Exercise 6

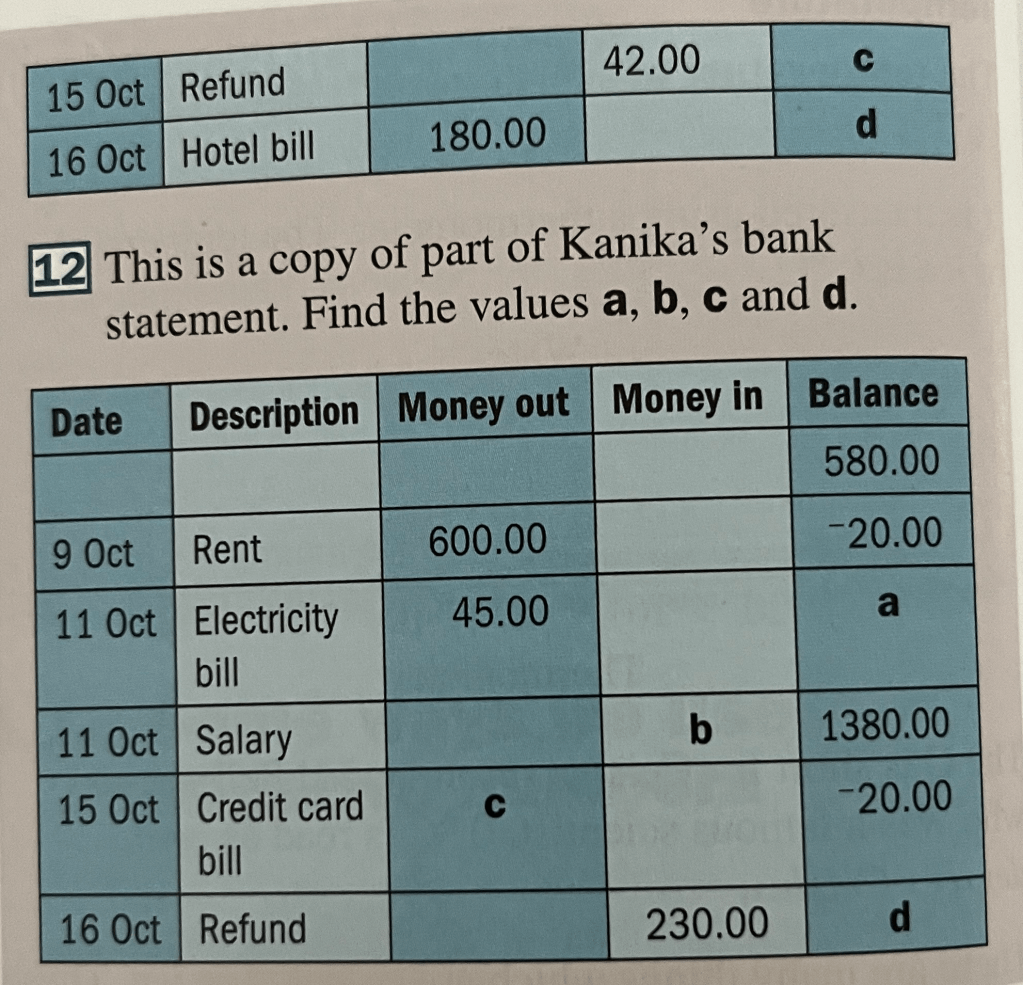
Exercise 7

Answers to all Exercises