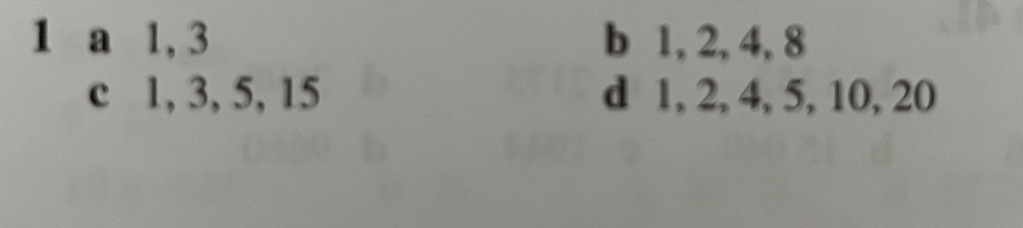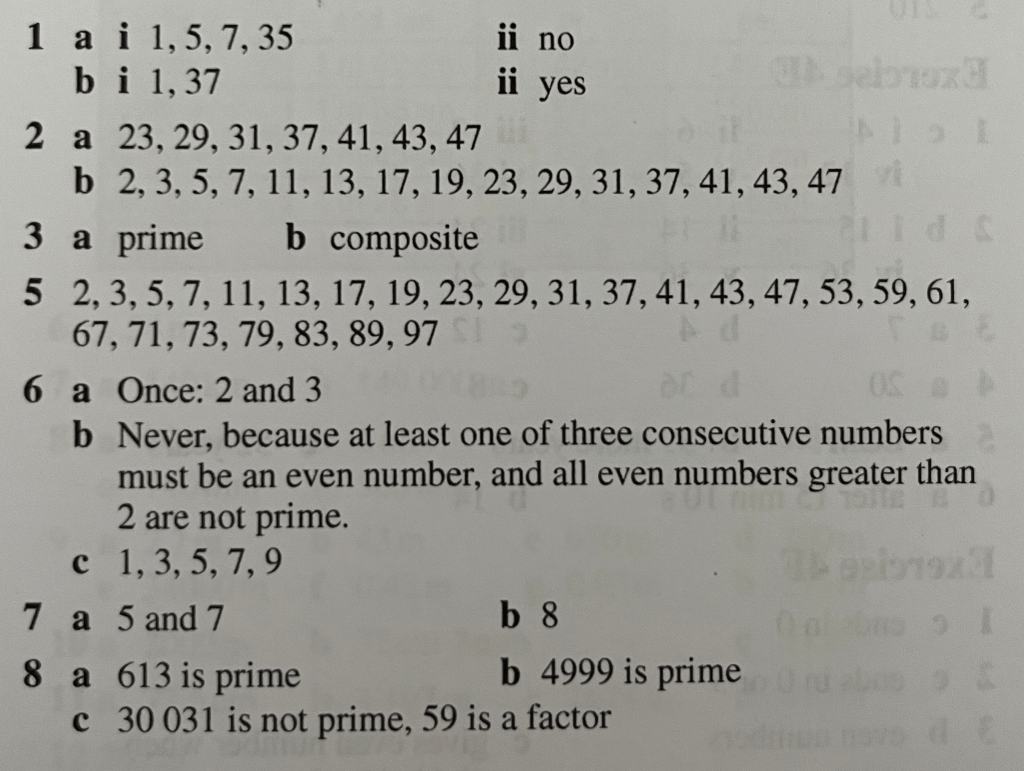Multiples

A multiple of a number is any number in its times table. So the multiples of 7 are 7, 14, 21, 28, 35, etc.

Exercise 1

Factors

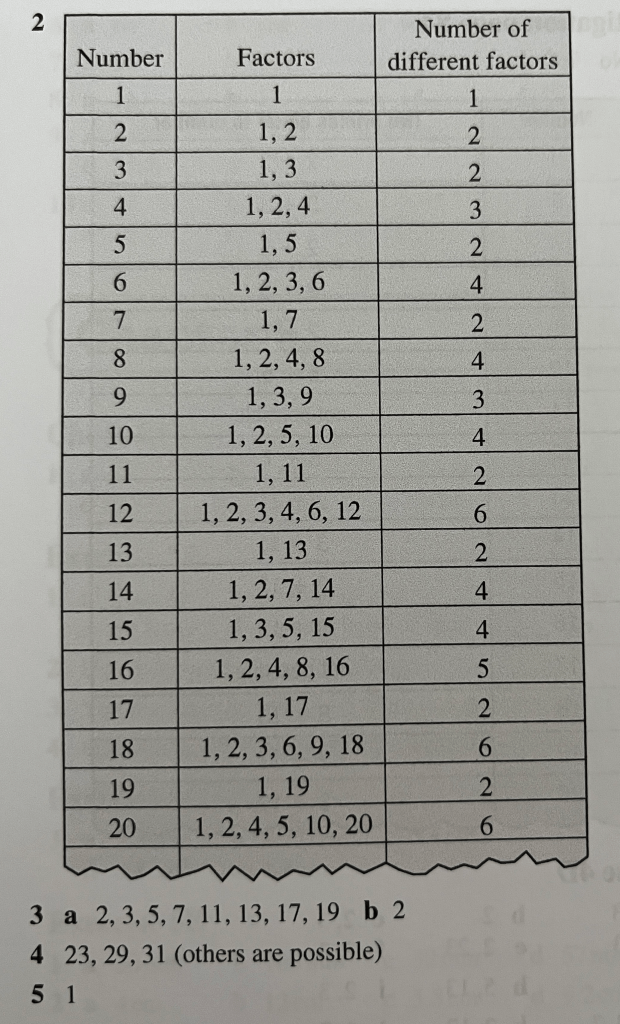
A factor is any number that divides a number without leaving a remainder. We can find them by trying to divide a number by each number in order. This gets quicker with practice as we start to quickly spot which ones we don’t need to try.

Let’s use this approach to try and find all of the factors of 36.

Exercise 2

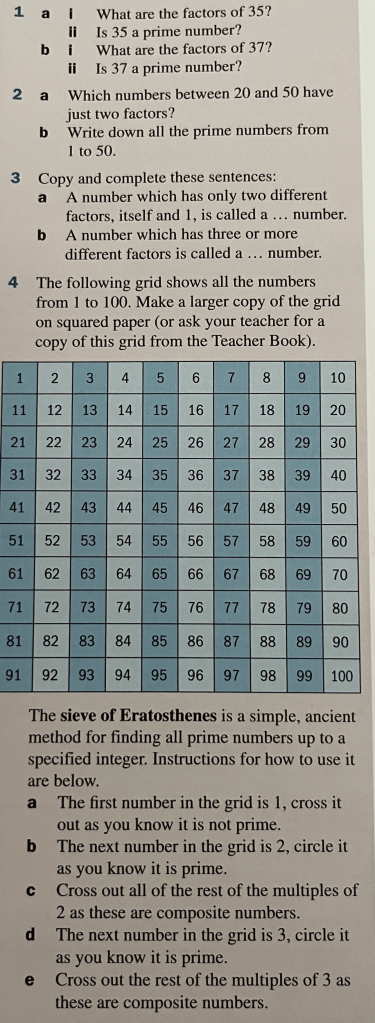
Prime Numbers

A prime number is one of the most important types of number in mathematics. It is a number with exactly two factors. One example is 13, because its only factors are 1 and 13. Which other examples can you think of.

A composite number is any number other than 1 which is not a prime number. So it has more than two factors. 8 is a good example, because with factors of 1, 2, 4 and 8 it is a composite number.

The number 1 is not a prime number and also not a composite number.

Exercise 3

Prime Factors

It can be very useful to identify the prime factors of a number – in the future this will help us solve lots of problems. Let’s learn a technique that will achieve this for us and then use it in the following exercise

Exercise 4

Highest Common Factors (HCFs) and Lowest Common Multiples (LCMs)

If we list out the factors of two different numbers and compare them, we can identify the highest common factor as the biggest number that is a factor of both of them. Let’s see how this works for 20 and 30.

If we list out some of the multiples of two different numbers, we can identify the lowest common multiple as the smallest number that is a multiple of both of them. Let’s see how this works for 6 and 8.

Exercise 5

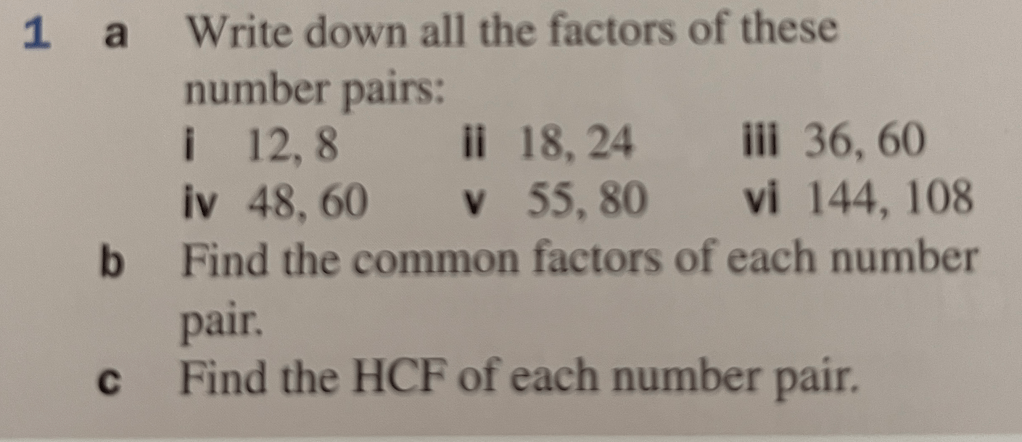
Answers to the five exercises above