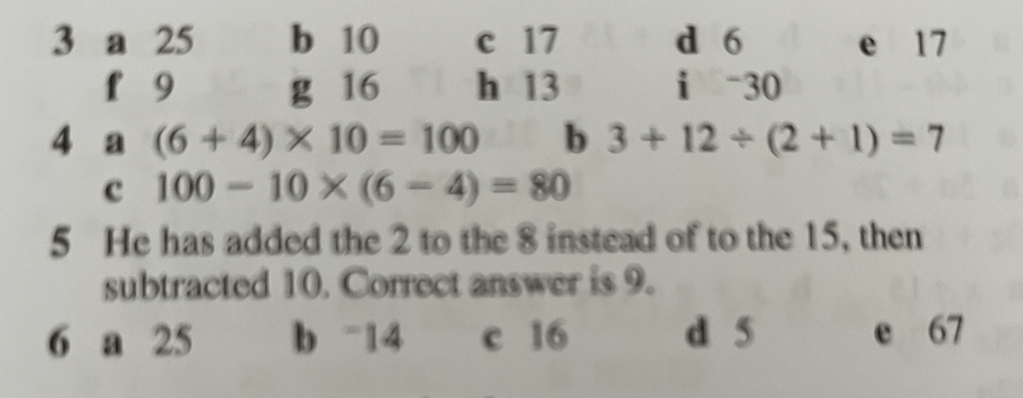• There are certain “laws” of arithmetic that we use all the time but often don’t know their names. Below are their names:
  • Commutative law: When we add or multiply numbers the order we do it in doesn’t matter. So 2 x 50 is the same as 50 x 2, and also 3 + 9 is the same as 9 + 3
  • Associative law: If we add or multiply together more than two numbers, it doesn’t matter which ones we do first. So if we have the calculation 3 x 5 x 2, we can calculate it as 15 x 2 or as 3 x 10. One way to say this is that (3 x 5) x 2 is the same as 3 x (5 x 2). The same logic applies with 4 + 2 + 9.
  • Distributive law: This is the only “law” that combines addition and multiplication. It tells us that 3 x (5 + 2) is the same as 3 x 5 + 3 x 2. It can be helpful to think of this geometrically.

Let’s look at how knowing these laws can make our life a bit easier with some calculations

Worked Example

• Calculate
  • 26 + 97 + 74
  • 23 x 25 x 2 x 2
  • 25 x (100 + 4)

Inverse Operations

This is another situation where we often do something but don’t know what it is called.

We can say that addition and subtraction are inverse operations because they “undo” each other (i.e. 2 + 3 – 3 = 2). The same applies with multiplication and division. We can see this working in a slightly different way in the example below.

Worked Example

• If 245 x 19 = 4655, then what is
  • 4655 ÷ 19?
  • 4655 ÷ 245?
• Complete the following:
  • 72 + ___ = 104
  • ___ ÷ 15 = 8

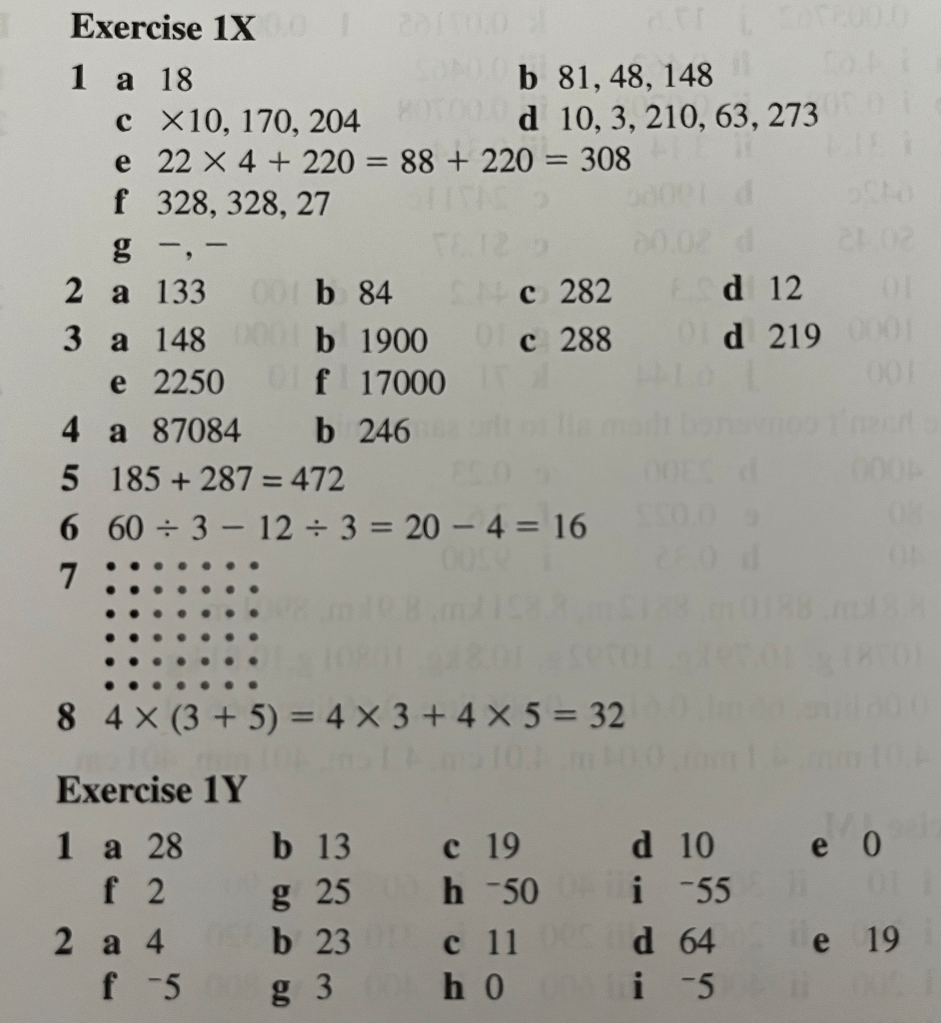
Exercise 1

Order of Operations

We have a special rule called BIDMAS that helps us to remember the order that we have to do arithmetic operations in. We don’t just work from left to right when doing them. Let’s practice this rule in the following examples.

Worked Example

• Calculate
  • 14 – 2 x (5 + 1)
  • (10 – 3) + 20 ÷ 4

Exercise 2

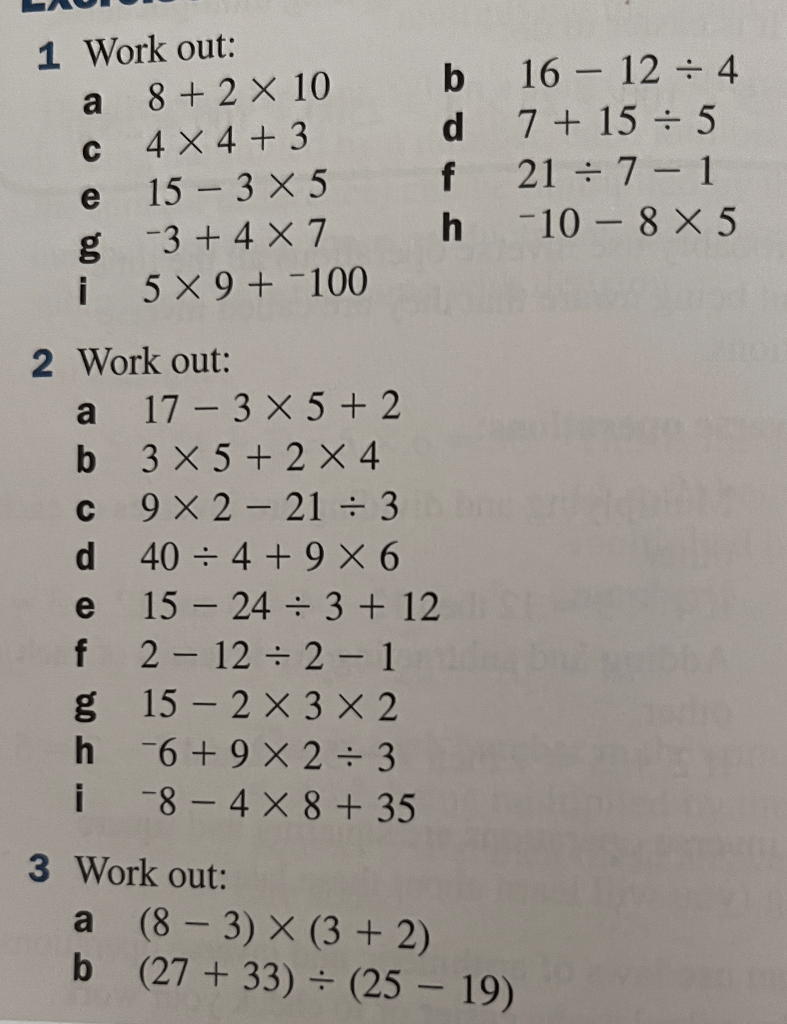
Answers to the two exercises above