Often in life we want to compare two quantities: Who is tallest? Who ran faster? Who got a higher score?

We can use the phrases is greater than or is less than to compare numbers

So, if I wanted to compare the numbers 68 and 66, what are two sentences I could use using the above underlined phrases to compare them.

We can also use the “crocodile signs” < and > to do this. How would you do that for the above numbers.

Short Exercise

1.) Make two sentences for each of the number pairs, using the phrases “is greater than” and “is less than”.

(a.) 1/8, 1/9   (b) 3/8, 0.4    (c) 3/7 , 4/9    (d) 0.7, 3/4

2.) Make two algebraic statements for each of the number pairs, using the symbols “<” and “is less >”.

(a.) 1/2 , 0.3   (b) 0.4, 1/3    (c) 1/8, 0.13    (d) 12/30, 5/12

3.) Write out the following statements, replacing the “…” with one of the phrases “is greater than”, “is less than” or “is equal to”

(a.) The number of bicycles in Beijing … the number of students in our class;

(b.) The number of questions in this exercise … the number of bakeries in Georgia;

(c.) The number of chairs in this room … the number of tables in this room.

Exercise

Ratios

A ratio is a convenient way of comparing amounts

So if we have a rule that for every two children that enter a shopping mall there must be one adult with them, we can say that the ratio of children to adults must be 2:1

Or if a cake is made such and for every 2 eggs it must have 3 sugar cubes, we can say that the ratio of sugar cubes to egges in the cake is always 3:2. Note that this is helpful regardless of how big a cake we want to make.

Exercise 2

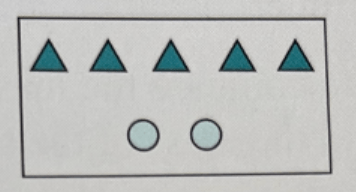
1.) Compare the number of triangles and circles in the diagram below and then copy and complete the following two statements:

(i.) For every … triangles there are … circles;

(ii.) For every … circles there are … triangles.

2.) Repeat this exercise for each of the following four diagrams:

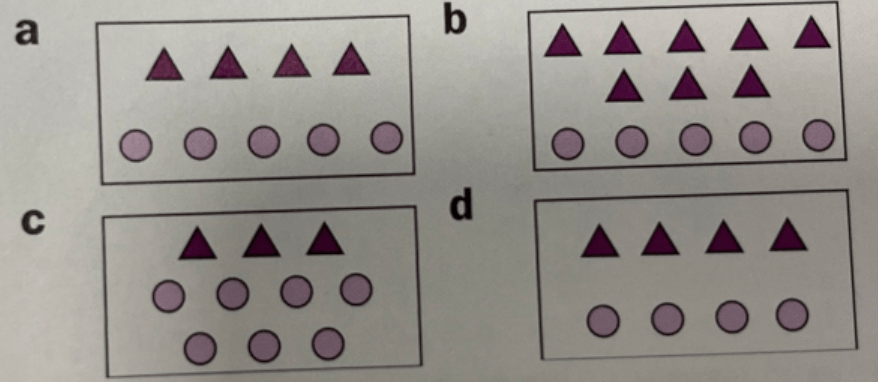
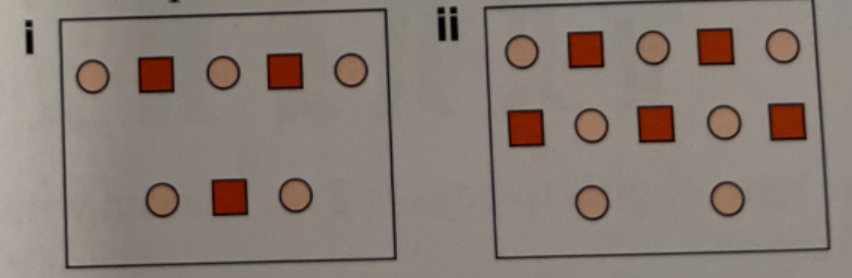
3.) In the following diagrams, write down a ratio to compare:

(a) The number of squares to the number of circles;

(b) The number of circles to the number of squares.

4.) The ratios below compare numbers of black circles to numbers of white circles. for each ratio, draw a diagram to illustrate this ratio:

(a.) 3:2   (b.) 1:5   (c.) 7:4   (d.) 5:9

5.) For the students in your class, use a ratio to compare:

(a.) The number of boys to the number of girls;

(b.) The number of girls to the number of boys;

(c.) The number of people with long hair to the number with short hair;

(d.) The number of people who have finished this exercise to the number that haven’t.

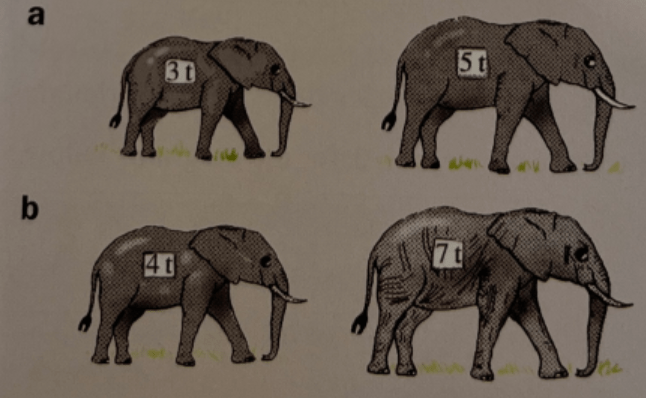
8.) Use a ratio to compare the mass of the first elephant with the mass of the second:

Answers to both exercises

Exercise 1

1.) (a.) 1/8 is greater than 1/9   (b) 3/8 is less than 0.4    (c) 3/7 is less than 4/9    (d) 0.7 is less than 3/4

2.) (a.) 1/2 > 0.3   (b) 0.4 > 1/3    (c) 1/8 < 0.13    (d) 12/30 < 5/12

3.)

(a.) The number of bicycles in Beijing is greater than the number of students in our class;

(b.) The number of questions in this exercise is less than the number of bakeries in Georgia;

(c.) The number of chairs in this room is equal to the number of tables in this room.

Exercise 2