Sometimes we can use quick methods to multiply or divide numbers, and sometimes we use more systematic formal methods.

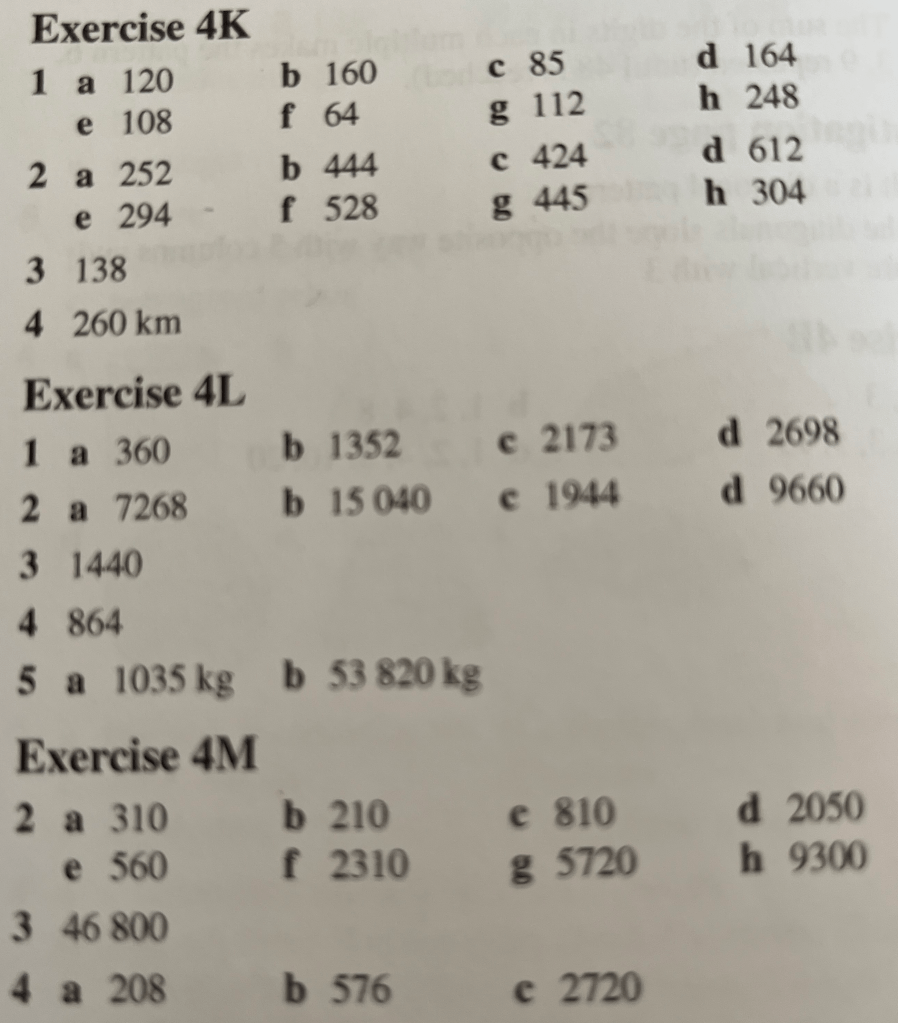
Let’s start with some quick and clever tips.

Multiplying by 5. Because 5 is half of 10, we can just multiply by 10 and then halve then answer.

Multiplying by 4. Because 4 is twice 2, we just double the number twice

Multiplying by 8. Because 8 is twice 4, we just double the number three times.

Distributive Law. We can use the distributive law, so for instance if we want to multiply a number by 15, we can multiply it by 10, separately multiply it by 5 and add the two results together.

Worked Examples

• Calculate:
  • 18 x 5
  • 33 x 4
  • 23 x 8
  • 7 x 18

Exercise 1

Formal Multiplication

Our formal method for multiplication relies on the distributive law, as we basically break the number up into units, tens, hundreds and thousands (depending how big it is), then systematically multiply each of these. Let’s look at the process to calculate 24 x 18.

There are alternative methods, such as the grid method. If you prefer to use this or any other formal method that is okay, but you do need to know at least one formal method for multiplying numbers together.

Exercise 2

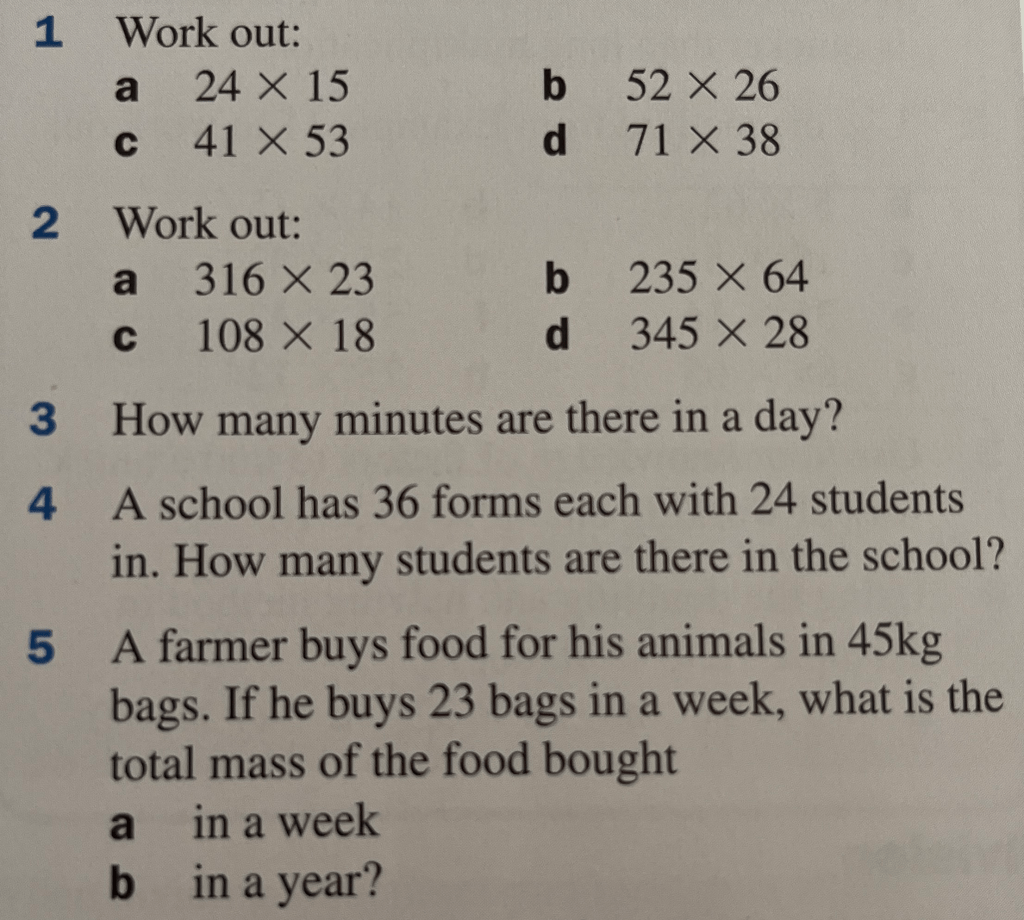
Using factors

Knowing how a number can be broken out into factors can help us with multiplying numbers. For instance, 15 x 28 can be made easier if we spot that 28 = 2 x 14.

There is also a useful method called the doubling/halving method. With this we halve one of the numbers and double the other one to get a different calculation with the same result. Consider using this to help with 14 x 16 for instance.

Exercise 3

• Use factors to help you calculate:
  • 5 x 62
  • 14 x 15
  • 15 x 54
  • 25 x 82
  • 35 x 16
  • 55 x 42
  • 88 x 65
  • 75 x 124
  • 45 x 65 x 16
• Use the doubling/halving method to calculate:
  • 13 x 16
  • 18 x 32
  • 17 x 160

Division

We need to have a formal method for division that doesn’t rely on a calculator. Let’s try using long division and short division methods to calculate the following:

Worked Example

• Calculate:
  • 938 ÷ 14
  • 8448 ÷ 24
• If a box can hold 25 sweets. How many boxes are needed to pack 434 sweets?
• If a cushion needs 54 cm of fabric and I have 9m of fabric, how many cushions can I make?

Exercise 4 (strictly no calculator)

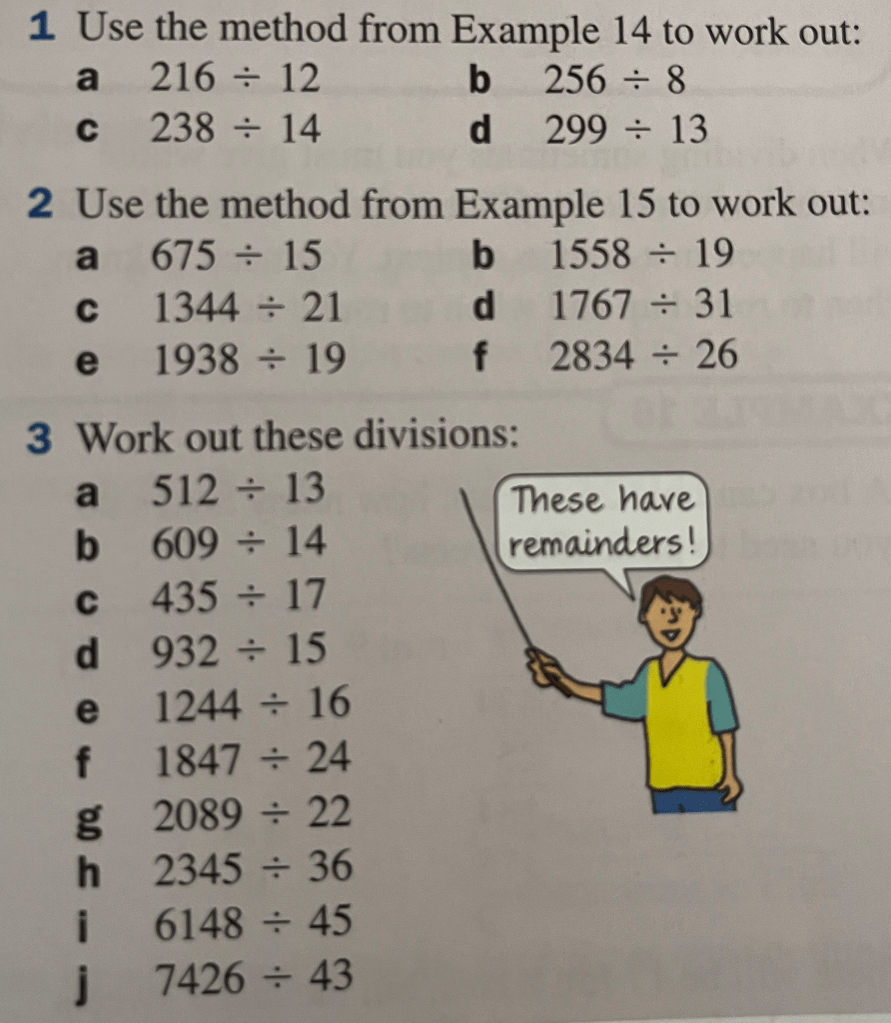
Answers to all four exercises