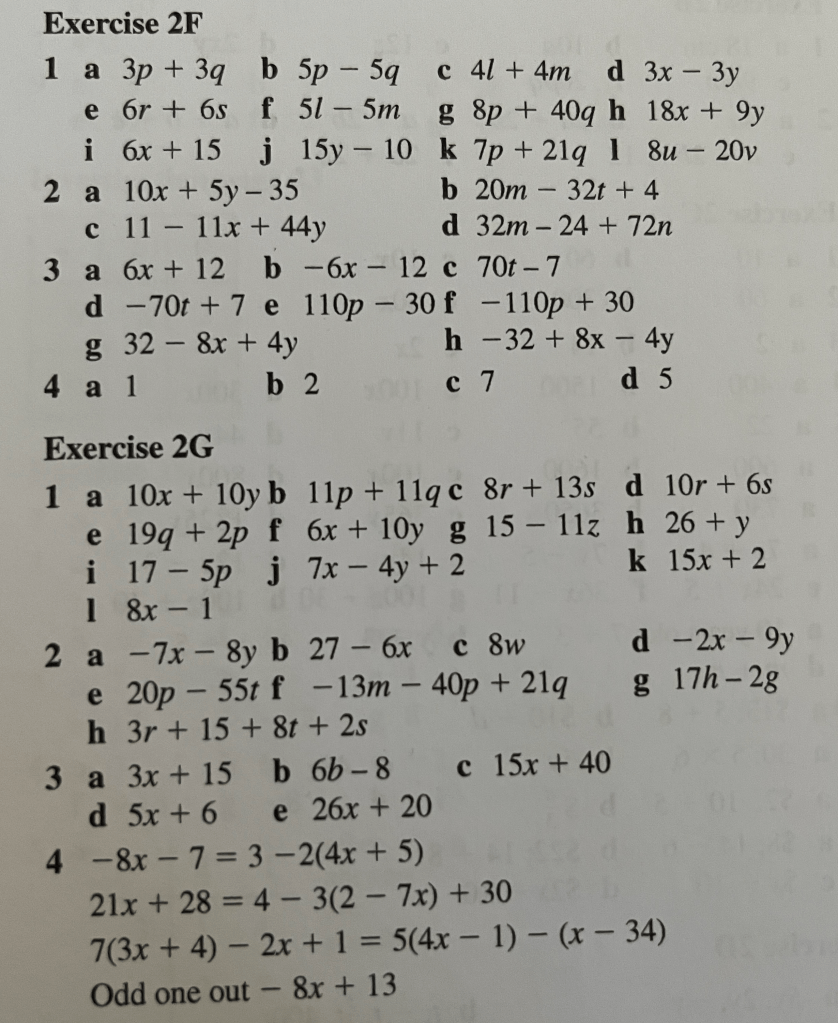We learned about the distributive law with arithmetic, where 3(2 + 4) is the same as 3 x 2 + 3 x 4. Any rules that apply with arithmetic also apply with algebra (as algebra is effectively a more generalised form of arithmetic. So 3(y + z) is the same as 3 x y + 3 x z, which we write as 3y + 3z. Similarly, y(a+b) = y x a + y x b, which we write as ya + yb, or even better as ay + by.

Worked Example

• Expand the brackets:
  • 5(6x – 3y)
  • 4(3p – q + 5)
  • -2(4y – 8)

Exercise 1

Order of Operations

When the expressions become a little more complicated we also need to remember BIDMAS.

Worked Example

• Simplify
  • 4y + 2 x 3y + 8y
  • 4t + 5(3p + 2t) – 4p
  • 6(2y – z) – 3(5y + 2z)

Exercise 2

Answers to both exercises