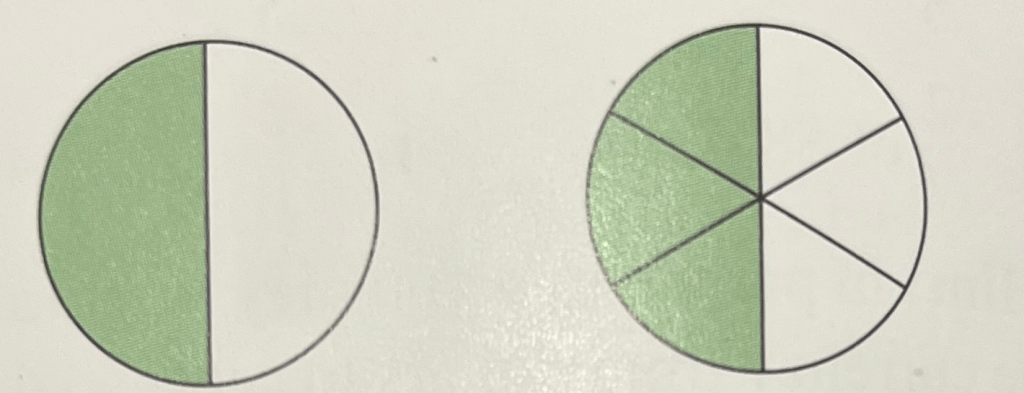
Notice that in the two circles below the same amount is shaded, despite the circles being separated in different ways. What can this tell us about equivalent fractions.

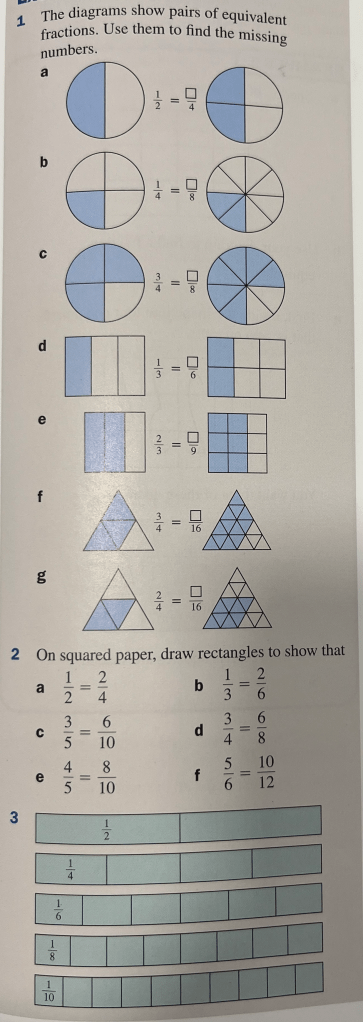
Let’s look at some fractions and find other fractions that are equivalent to them.

Exercise 1

Fraction Walls

A fraction wall can help us find equivalent fractions

Worked Example

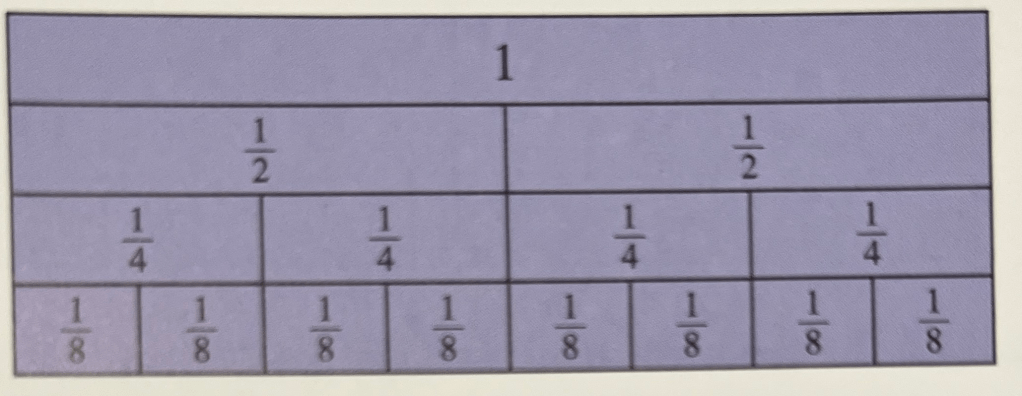
• Use the fraction wall above to:
  • Write down a fraction equal to 3/4
  • Write down two fractions greater than 1/2

Exercise 2

Fractions of Shapes

Looking at fractions of shapes can help us to identify equivalent fractions

Worked Example

Shade 3/4 of the shape above.

Use the diagram to find a fraction equivalent to 3/4

Exercise 3

Calculating Equivalent Fractions

We don’t need to draw a diagram every time we want to calculate an equivalent fraction.

As long as we multiply the numerator and the denominator by the same amount, the fractions will be equivalent.

So if we are told the denominator we want, then we just need to calculate what our denominator is multiplied by and multiply the numerator by the same.

Worked Example

What value should replace the question mark: 3/4 = ?/24

Exercise 4

Simplifying Fractions

Of all the different equivalent fractions, we prefer the simplest form, which is where the numerator and the denominator have no common factors (they are both as small as can be).

To write a fraction in simplest form, we divide the fraction we have by the HCF of its numerator and denominator.

Alternatively, instead of calculating the HCF, we can just keep dividing them by any common factors until there are no more common factors to divide them by.

Worked Example

Write 36/48 in simplest form

Exercise 5

Answers to all five exercises