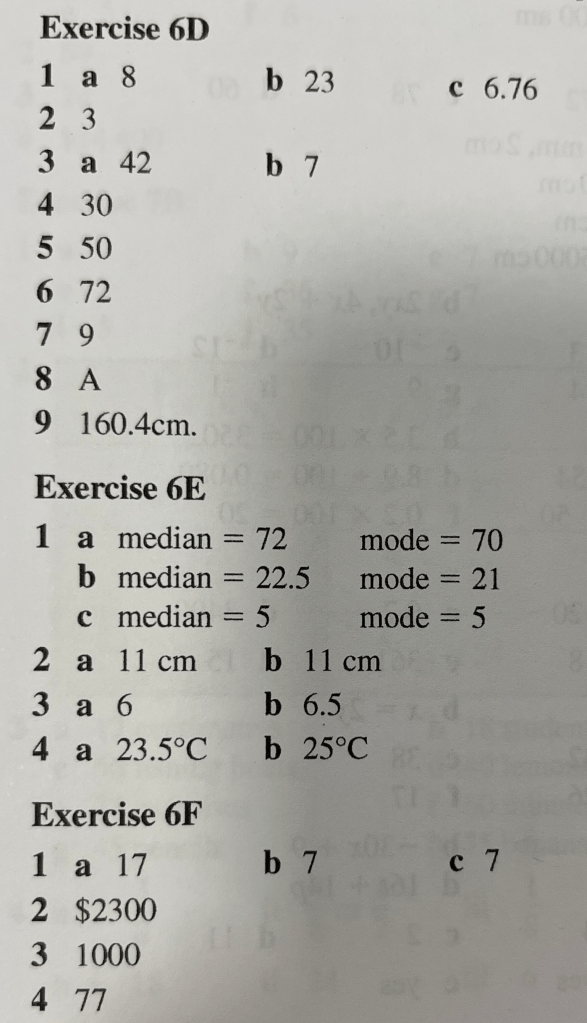An average is a single number that is used to represent a whole dataset. So for instance, we could represent the whole dataset 1, 2, 3, 4, 5 with the single number 3.

There are different averages that serve as better representatives of datasets in different situations. They are the mean, the mode and the median.

The mean

In typical conversations, when people refer to an average they are normally referring to the mean. We calculate the mean by adding up all of the values in a dataset and dividing the total by the number of values. Let’s try calculating it for some datsets.

Exercise 1

Other Averages: Mode and Median

Whilst the mean is the most important single average, we need to know about these other averages to.

The mode is the data value in the dataset which occurs most often. So in the dataset 1, 2, 2, 3, 4, 5, 6, the mode is 2. Clearly some datasets don’t have a mode. We also call some datasets bimodal.

Worked Example

On Friday, Billy’s Shoe Shop sells shoes with the following sizes: 6, 7, 7, 5, 8, 9, 8, 9, 9 and 5. Shat was the modal shoe size sold?

The median is the middle value of a data set if all the numbers are put in order. If there is no middle value (this will happen if there are an even number of values in the dataset), then the median is the average of the middle two values.

Worked Examples

1.) Find the median of the test scores: 3, 8, 4, 5 and 9;

2.) Find the median of the temperatures: 16º, 23º, 20º, 18º, 17º and 25º.

Exercise 2

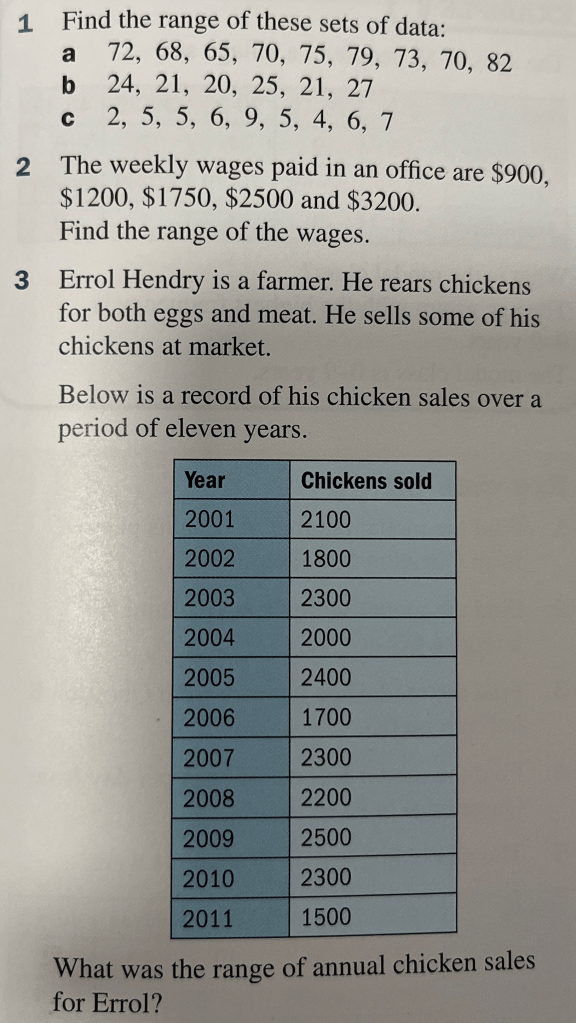
Range

The range is not an average, it is a measure of spread – it tells us how spread out the data is.

We calculate it by subtracting the smallest number in the dataset from the largest number.

Worked Example

Find the range of the following data: 2, 11, 7, 3, 2, 8 and 4.

Exercise 3

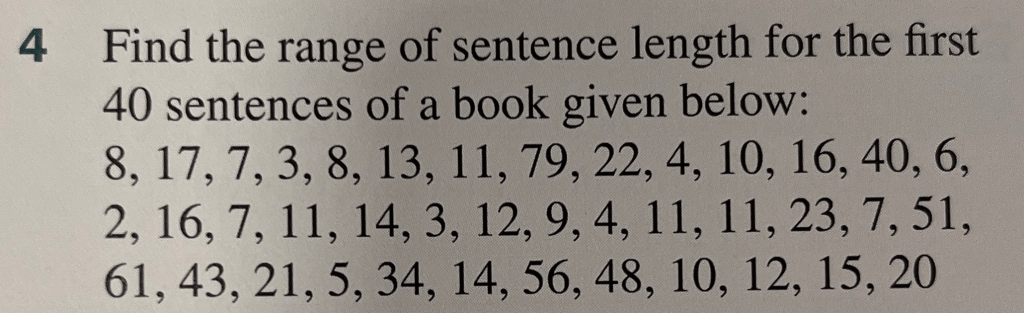
Answers