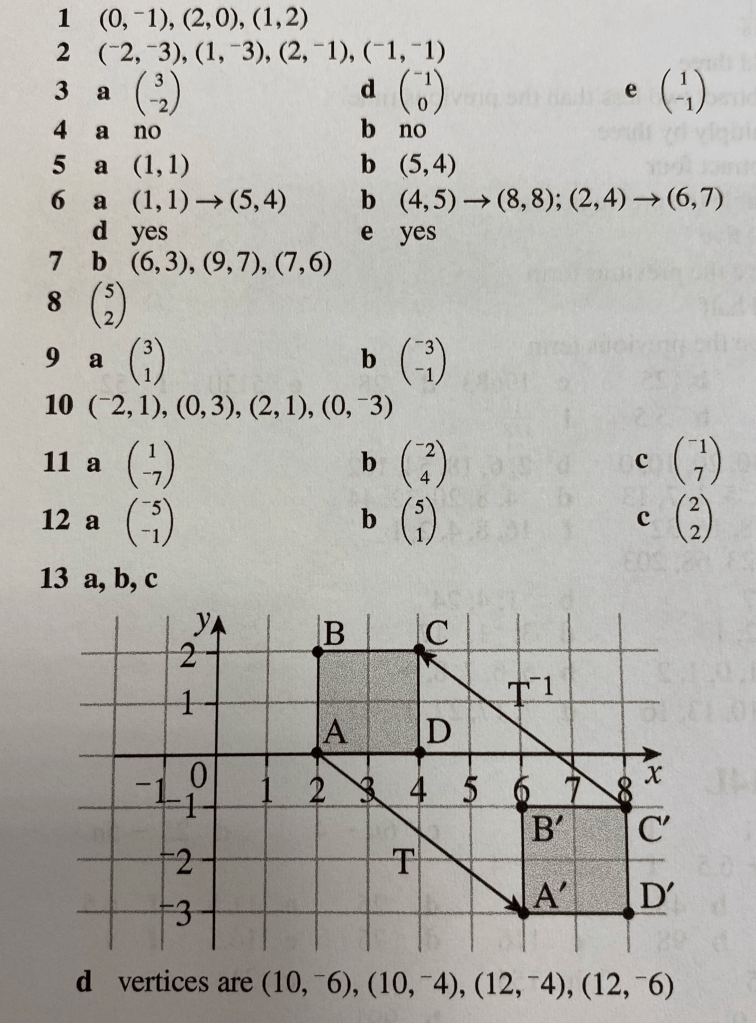Maths with David

    Y9. Translations

    One of the easiest kinds of geometrical transformation is a translation. This basically involves moving a shape.

    We need to know how to use column vectors to describe a translation. Also, if we are given a column vector we should be able to draw the image after a translation has taken place.

    We should be able to apply a translation (if we know the column vector) to information given in coordinate form and to information given in graphical form.

    Example

    Exercise

    1. The vertices of triangle PQR are (-4,2), (-2,3) and (-3,5) respectively. Determine the vertices of the image triangle P’Q’R’ under the translation \textbf{T} = \begin{bmatrix} 4 \\ -3 \end {bmatrix} .
    2. The vertices of a parallelogram ABCD are (1,1), (4,1), (5,3) and (2,3) respectively. Find the vertices of the image of the parallelogram under a translation \textbf{T} = \begin{bmatrix} -3 \\ -4 \end {bmatrix}
    3. The diagram below shows a triangle ABC:

    Copy the diagram into your book. On your copy also draw the triangles listed below in parts (a) to (e). If any of the extra triangles you draw are translations of ABC, then write down the column vector of the translation:

    • (a) (4,-1), (7,3), (5,2)
    • (b) (2,1), (4,2), (5,5)
    • (c) (0,0), (0,3), (2,4)
    • (d) (0,1), (1,4), (3,5)
    • (e) (2,0), (3,3), (5,4).

    4a. Are all of the triangles in question 3 the same shape and size as triangle ABC?

    4b. If two triangles are the same shape and size as each other, does it mean that one is definitely a translation of the other?

    5. The vector \begin{bmatrix} 4 \\ 3 \end {bmatrix} maps the triangle ABC to its image PQR. Point A maps to P, as shown in the diagram below:

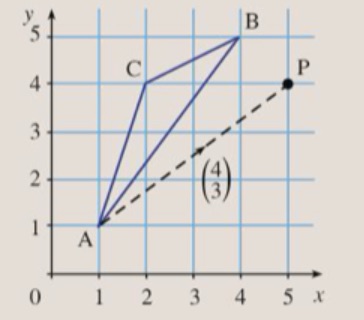
    a.) What are the coordinates of A?

    b.) What are the coordinates of P?

    c.) Given the translation vector and the coordinates of A, explain how to find the coordinates of P without using a diagram.

    6a. Copy and complete the following (it relates to question 5 above):

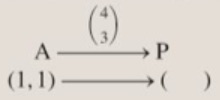
    6b. Show the mappings B -> Q and C -> R in the same way as the above shows the mapping A -> P.

    6c. On squared paper draw a pair of axes marked with steps from -1 to 10. Draw on it the triangles ABC and PQR.

    6d. Does a translation map all points the same distance and in the same direction?

    6e. Is triangle ABC the same shape and size as its image, PQR?

    7. Another translation maps the triangle PQR from question 5 above to image triangle STU. The vector for the translation is \begin{bmatrix} 1 \\ -1 \end {bmatrix} .

    7a. Show STU on your diagram for question 6

    7b. Write down the coordinates of S, T and U.

    8. What is the translation vector that maps triangle ABC to triangle STU (in questions 7).

    Copy and complete the following: \begin{bmatrix} 4 \\ 3 \end {bmatrix} + \begin{bmatrix} 1 \\ -1 \end {bmatrix} = \begin{bmatrix} ? \\ ? \end {bmatrix}

    9. X, Y and Z are three points. The vector \begin{bmatrix} 2 \\ 7 \end {bmatrix} maps X to Y and the vector \begin{bmatrix} 1 \\ -6 \end {bmatrix} maps Y to Z.

    a. What single vector maps X to Z?

    b. What vector would map Z to X?

    10. A kite ABCD is mapped under the translation \textbf{T} = \begin{bmatrix} 4 \\ 5 \end {bmatrix} to A’:(2,6), B’:(4,8), C'(6,6) and D'(4,2). Determine the vertices of the kite ABCD.

    11. On graph paper, draw the triangle MNO with vertices M(1,1), N(3,3) and O(3,-1). Translate the triangle MNO using the vector \begin{bmatrix} 2 \\ -4 \end {bmatrix} . Label the vertices of the image M’N’O’.

    Translate the triangle M’N’O’ using the vector \begin{bmatrix} -1 \\ -3 \end {bmatrix} . Denote this new image M”N”O”. Label the vertices of M”N”O”. Give the vectors describing the translations which map:

    a. Triangle MNO to triangle M”N”O”

    b. Triangle M’N’O’ to triangle MNO

    c. Triangle M”N”O” to triangle MNO.

    12. On graph paper, draw the rectangle ABCD with vertices A(2,1), B(2,-1), C(-2,-1) and D(-2,1). Translate ABCD with the vector \textbf{T} = \begin{bmatrix} -3 \\ 1 \end {bmatrix} . Denote the image of ABCD as A1B1C1D1. Then translate A1B1C1D1 using the vector \textbf{T} = \begin{bmatrix} -2 \\ -2 \end {bmatrix} . Denote this new image A2B2C2D2. State the vertices of A1B1C1D1 and A2B2C2D2. Give the vectors that translate:

    a. ABCD to A2B2C2D2

    b. A2B2C2D2 to ABCD

    c. A2B2C2D2 to A1B1C1D1

    The answers are below: