The idea of a ratio is similar to the idea behind scale factors and is related to the idea of fractions. Students from some countries must be careful with the notation, because in English we use the symbol : to represent a ratio (and not division)

If Ann and Bob have money in the ratio 2:3, it means that for every $2 that Ann has, Bob has $3. Another way of saying this would be to say that for every $5 the people have, $2 of them are Ann’s and $3 of them are Bob’s.

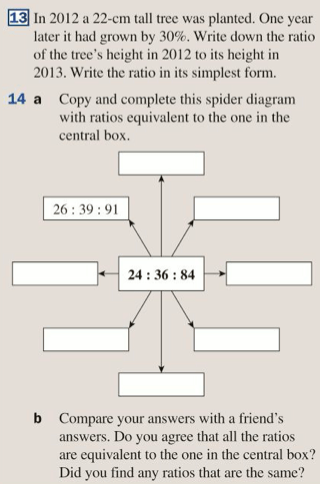
As with fractions, we should normally write a ratio in its simplest form, so our final answer should never be 4:6 or 20:30 or 14:21. They should also be written with integers, so we should never write 0.5:0.75. (Also note that ratios do not have units).

One of the advantages of simplifying ratios (as with fractions) is it is easier to compare them. If we know the ratio of Ann’s money to Bob’s money is 1:4 and the ratio of Ann’s money to Ivan’s money is 1:5, it is easier to see that Ivan is wealthier than Bob. But if we were told that the ratio of Ann’s money to Bob’s money is 6:30 and the ratio of Ann’s money to Ivan’s money is 7:28, it is not so easy to make this conclusion.

Example

Simplify the following ratios:

Exercise

Let’s complete exercise 13A on pages 209 and 210 of the textbook:

The answers are below: