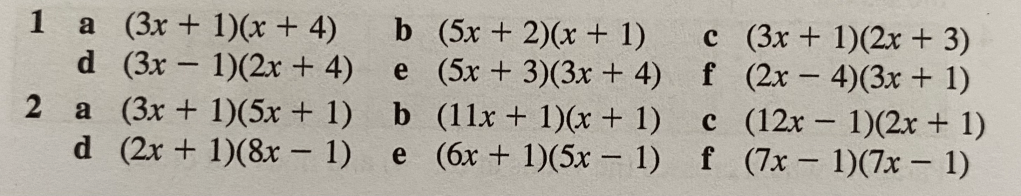There are several ways of factorising quadratic expressions that we will learn over time. The first method is a special case of Vieta’s Formula, which tells us that if we can find two numbers whose product is the constant and whose sum is the coefficient of x, then we can write the equation in factorised form.

As with most of mathematics, it is much easier to see what this means by way of example, so let’s look at the examples below together with the teacher. It is always easiest to start by considering the constant, and which factor pairs multiply together to give it, and then consider which of those factor pairs sum to give the coefficient of x.

Examples

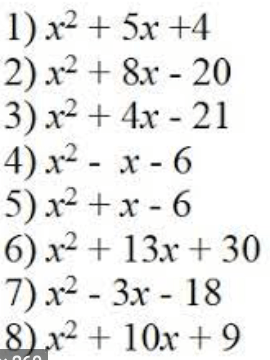
Exercise

Let’s complete exercise 19E from page 313 of the textbook:

The answers are below:

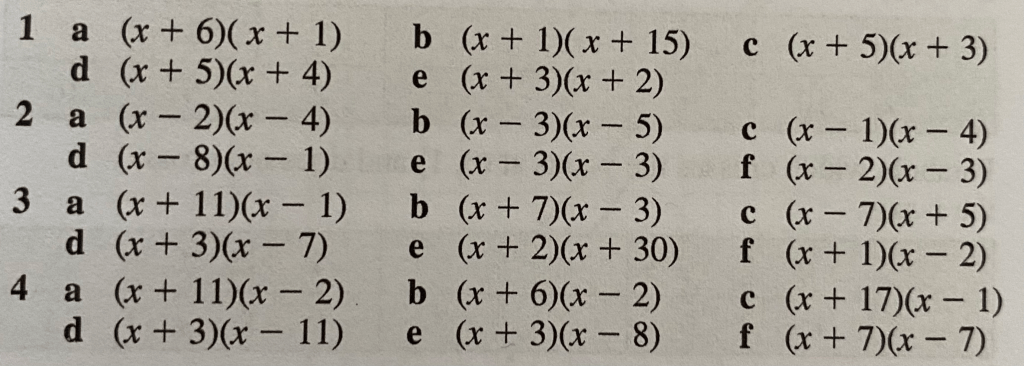
Factorising where x² has a coefficient

In the slightly more difficult situation where the x² term has a coefficient, we need to find two numbers whose product is equal to the product of the coefficient of x² and the constant. Once we have found these two numbers, we use them to split the “x-term” up into two parts and we can then factorise by first factorising the first two terms and the second two terms separately.

Let’s look at some examples to see this in practice:

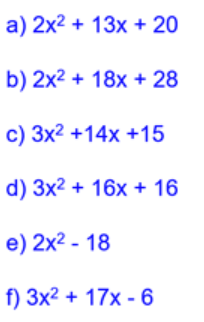
Exercise

Let’s complete exercise 19F from page 314 of the textbook:

The answers are below: