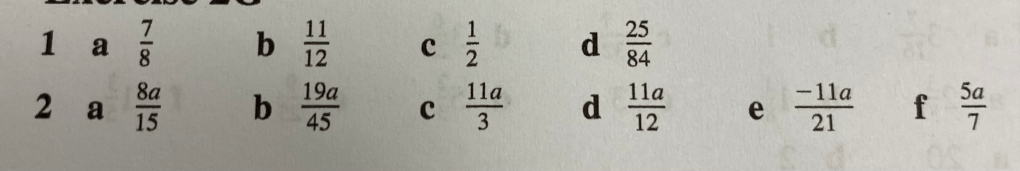Algebraic Fractions

In general, we find that all of the rules we have learned in arithmetic apply in the same way in algebra and this is also the case with algebraic fractions. Just as in arithmetic, in order to add or subtract fractions, we must first ensure that the denominators of the fractions are the same (they then have a common denominator)

To make the denominators of the fractions the same, we can multiply the numerator and the denominator of one or both fractions by any number (or letter, or expression) that we want (except for zero), the only rule being that we must multiply the numerator and the denominator by the same thing.

So, in order to do the addition: 1/21x + 4/21 , what would we need to do?

In order to calculate 1/x + 4/21 what would we need to do?

How about 1/x + 4/21 + 2/7?

How about with expressions. How would we calculate 1/(x+1) + 4/(x+2)

How about 1/(x+1) – 4/(x+2)?

Let’s try some together:

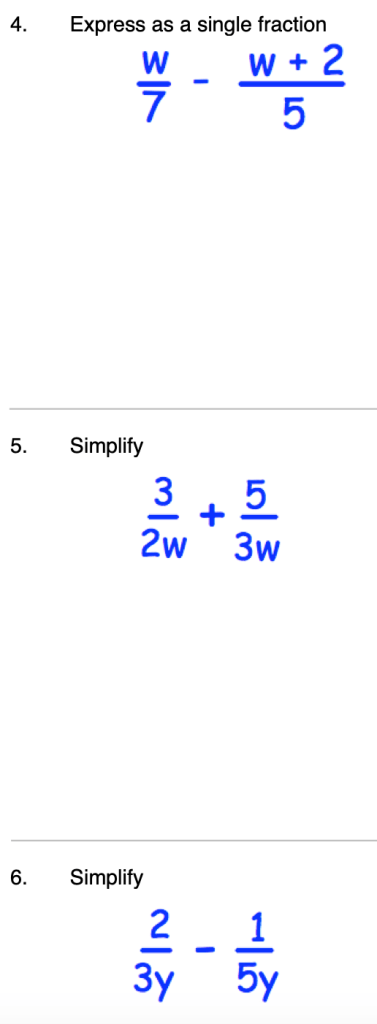
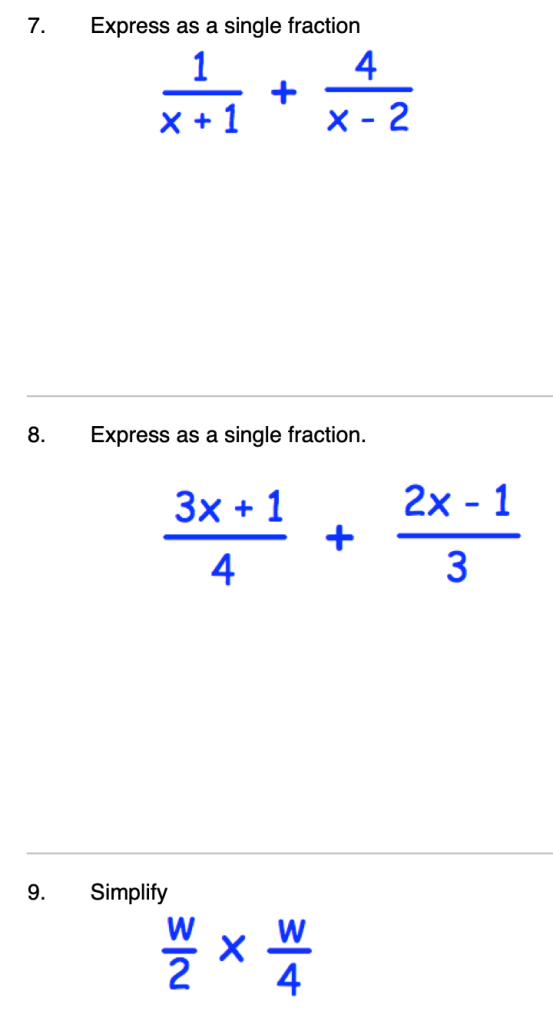
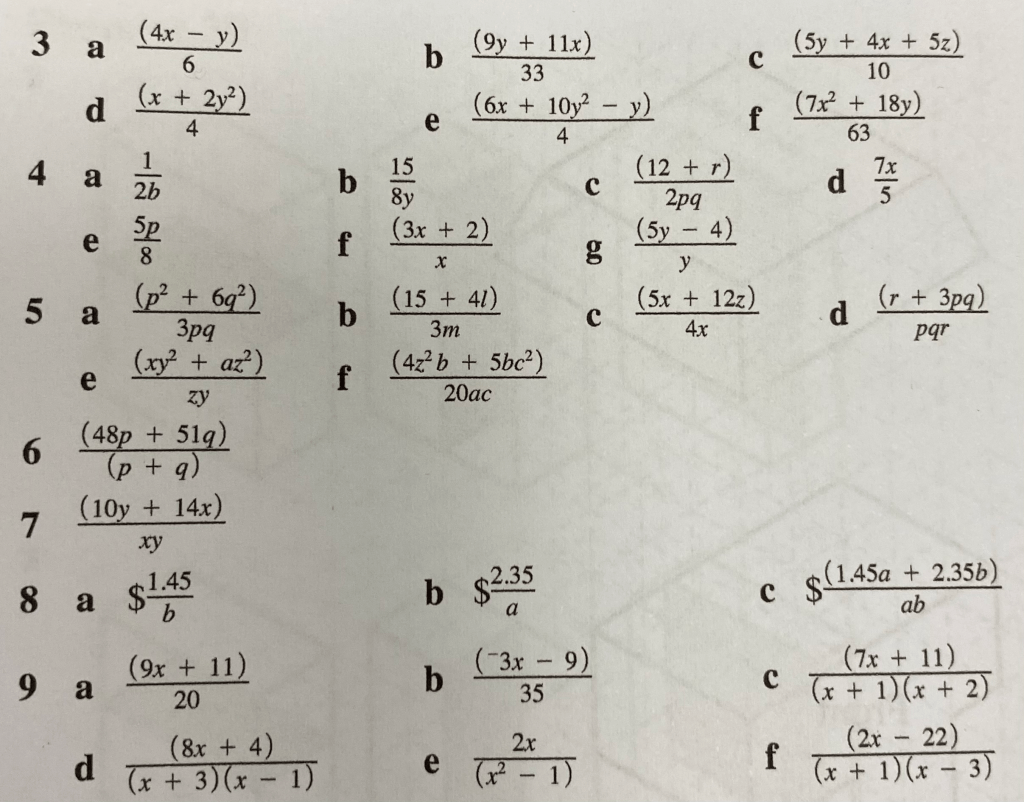
Here are some for you to try for yourself (from exercise 2G on pages 27 and 28 of your textbook)

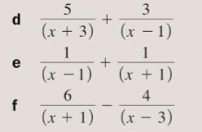
Below are the answers to the above questions: