Maths with David

    KS5. S1. Normal Distribution

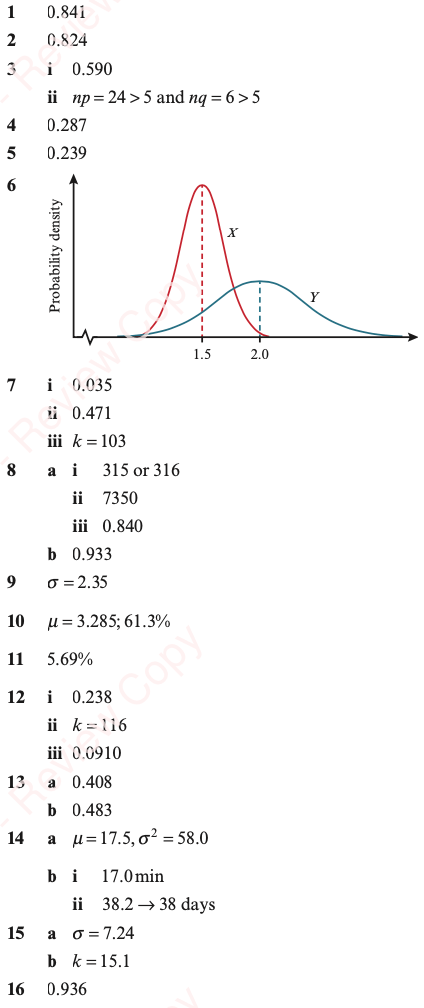
    What is a standard normal distribution?

    The standard normal distribution has mean 0 and standard deviation 1.

    Later we will learn how to convert any normal distribution to this “standard” normal distribution, which allows us to find the probabilities that X is below or above certain values.

    Like all probability distributions, the sum of the probabilities (represented by the area under the curve) is equal to 1.

    As this is a continuous distribution, it is only possible to find probabilities of intervals, not of specific points (the same as we can only measure a distance on a drawn line, not identify a specific point).

    The modal class is in the middle.

    The distribution is completely identified by N(mean,var).

    N.B. With continuous distributions the strictness of an inequality has no relevance.

    Some special features of a normal distribution:

    How to use a table of normal distribution values (provided in your MF19 book) to calculate probabilities – Worked Examples

    • Use the probability tables to calculate:
      • P(Z < 1.52)
      • P (Z < -0.75)
      • P (-1.18 < Z < 1.43)
      • P (X>1)
    • Use the tables “backwards” to find z such that P(Z<z)=94%.

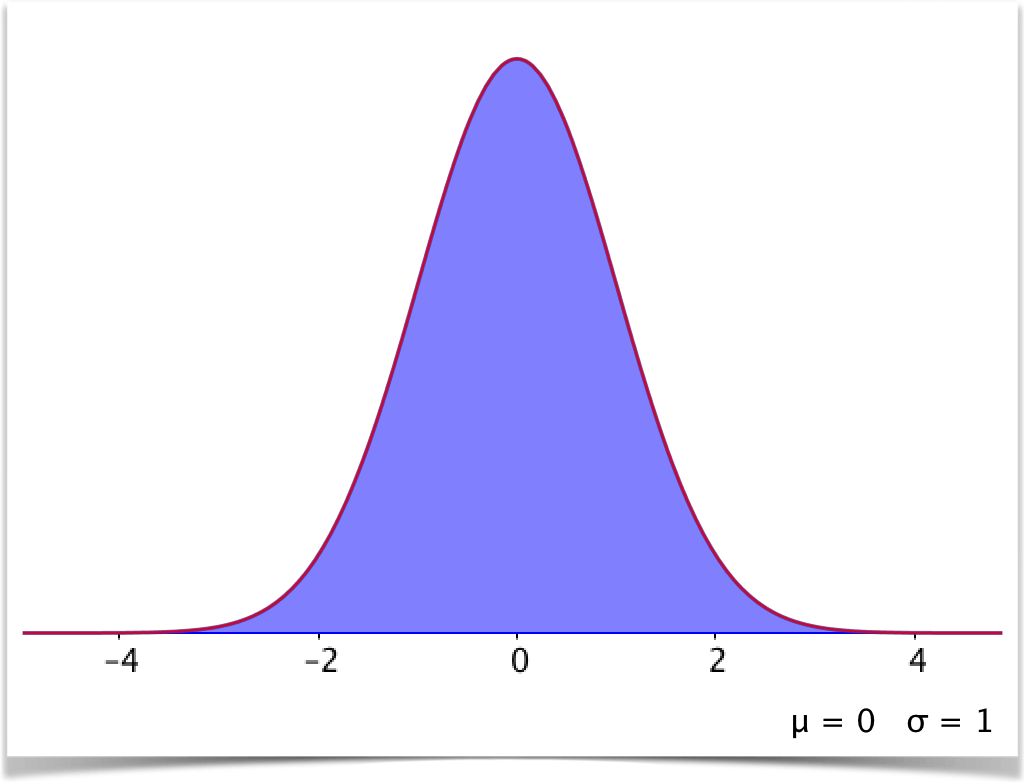
    Exercise 1

    Answers

    Exercise 1 Worked Solutions

    What is a normal distribution?

    If X is a normally distributed random variable, we write X \sim N(\mu,\sigma^2) , where \mu is the population mean and \sigma^2 is the population variance.

    Standardising the normal distribution

    Z = \frac{X- \mu}{\sigma}

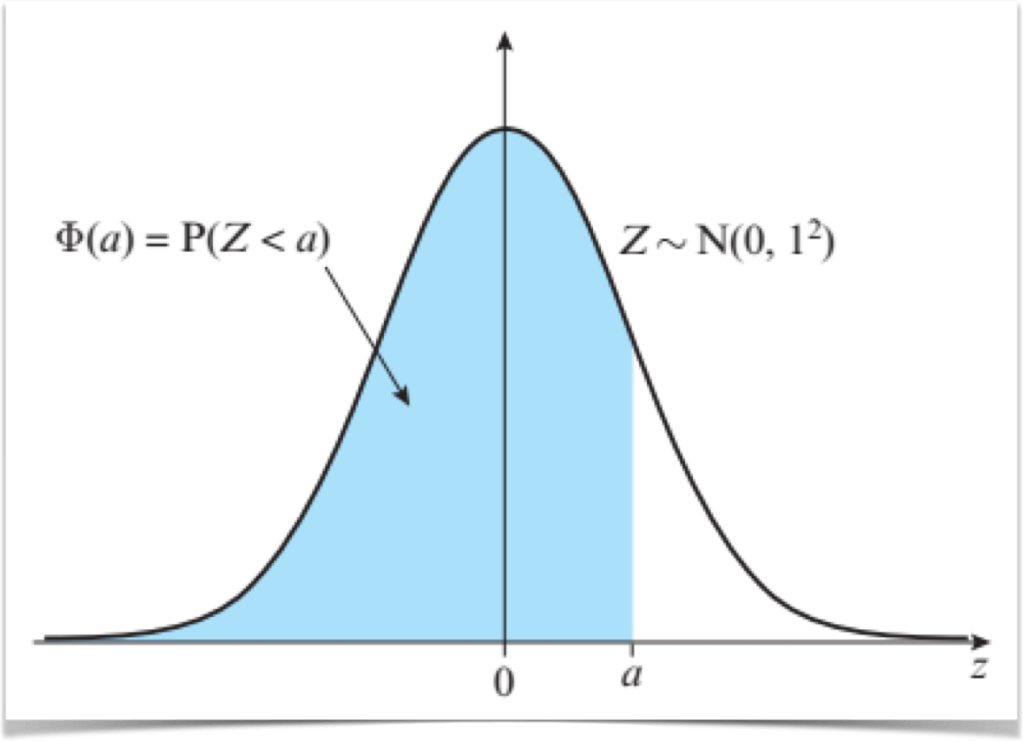
    Worked Examples

    • The random variable X \sim N(50,4^2). Write in terms of \Phi (z) for some value z:
      • P(X < 53)
      • P(X ≥ 55).
    • N.B. \Phi (z) is the notation we use to mean P(Z<z). We can also use the inverse of it, so if P(Z<z)=0.7, then \Phi^{-1} (0.7) will give us z.

    The random variable X \sim N(30,5^2) . Find the value of a to 2 decimal places, such that:

    a. P(X<A) = 0.75

    b. P(X>A) = 0.4

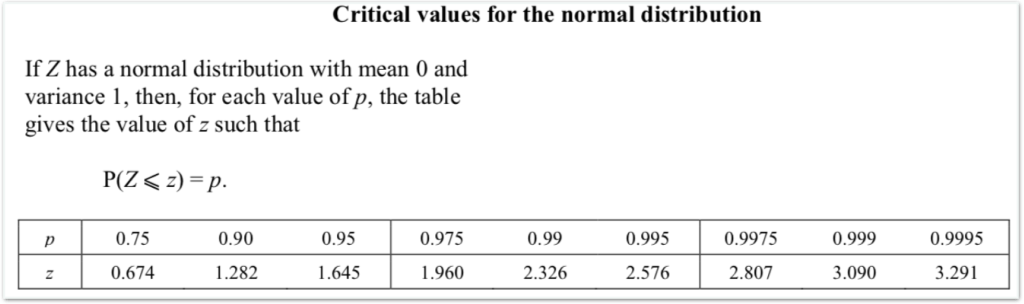
    N.B. For certain key values we can also use the “working backwards” table included in MF19 and extracted below:

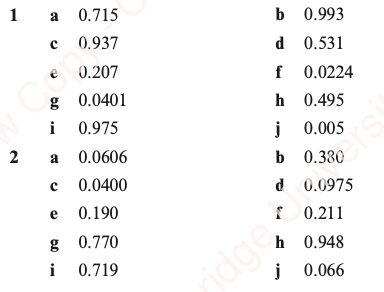
    Exercise 2

    Answers

    Exercise 2 Worked Solutions

    Applications

    Worked Examples

    The mass of a newborn baby in a certain region is normally distributed with mean 3.35 kg and variance 0.0858 kg2. Estimate how many of the 1356 babies born last year had masses of less than 3.5kg

    A factory produces half-litre tins of oil. The volume of oil in a tin is normally distributed with mean 506.18 ml and standard deviation 2.96 ml.

    1. What percentage of the tins contain less than half a litre of oil?
    2. Find the probability that exactly 1 out of 3 randomly selected tins contains less than half a litre of oil.

    Exercise 3

    Answers

    Exercise 3 Worked Solutions

    Using the normal distribution as an approximation to the binomial distribution

    For large numbers of trials, calculating the binomial distribution can be difficult (try calculating 100C24x0.324x0.776 on paper).

    However, as n becomes large, if the probability is close to 0.5, the distribution tends towards a normal distribution. In strict terms, we say that the normal distribution is a good approximation for the binomial distribution if np>5 and n(1-p)>5.

    Continuity Correction

    Because the normal distribution is continuous and the binomial distribution is discrete, we need to make a small adjustment when doing our approximation.

    A discrete value such as X=9 must be represented by the class of continuous values 8.5≤X<9.5.

    So, for instance, if we want to calculate P(X<13) on a binomial distribution, then we will calculate P(Y<12.5) on the normal distribution that we use to approximate it. Alternatively, if we want to calculate P(X≤13) we will calculate P(Y≤13.5).

    Worked Examples

    A. Given that X ~ B(100, 0.4), use a suitable approximation and continuity correction to find:

    a. P(X<43)

    b. P(X>43)

    B. Boxes are packed with 8000 randomly selected items. It is known that 0.2% of the items are yellow.

    Find, using a suitable approximation, the probability that:

    1. A box contains fewer than 20 yellow items
    2. Exactly 2 out of 3 randomly selected boxes contain fewer than 20 yellow items.

    C. A fair coin is tossed 888 times. Find, by use of a suitable approximation, the probability that the coin lands heads-up at most 450 times.

    Exercise 4

    Mixed Exercise

    Exercise Answers

    Mixed Exercise Answers

    Exercise 4 & Mixed Exercise Worked Solutions