KS5. 9709. Quadratics

First, let’s practice a 2016 exam question on topics already covered.

Mark Scheme

Equations

What does a quadratic equation look like algebraically (try to be as general as possible).

How many different ways do we know to solve quadratic equations?

How many different ways do we know to solve simultaneous equations (sometimes called a system of equations)?

When we are dealing with inequalities instead of equations, what additional considerations are needed when solving them?

Syllabus Extract

Below is an extract showing the Cambridge 9709 syllabus requirements regarding quadratic equations:

Completing the Square

Do you remember how to rewrite y=x²+4x+9 in completed square form?

Graphically, this equation represents a parabola. What are the coordinates of the vertex of the parabola.

Please try to draw a sketch diagram of the following quadratic equations:
- y = x² + 4x + 9;
- y = 3x² – 12x + 6.

How would things change if the leading coefficient were negative? (and what is a leading coefficient? 😉)

Worked Example

Sketch the graph of y = 16x – 7 – 4x²

Exercises 1 and 2

Answers

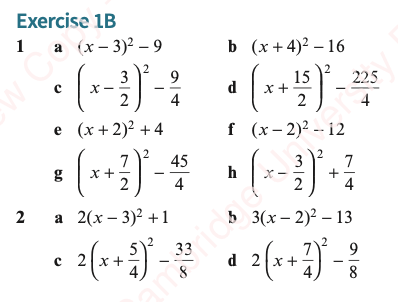
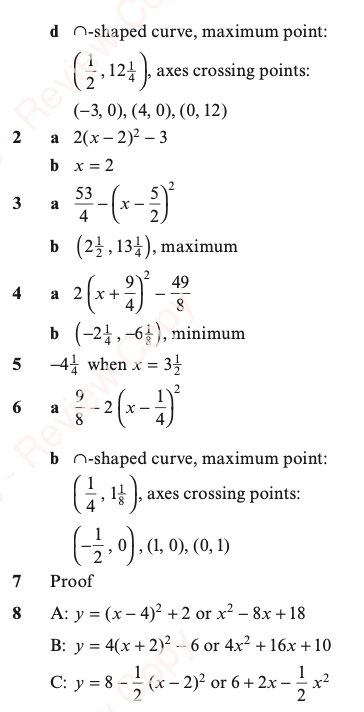
Exercises 1 and 2 Worked Solutions

Using the Discriminant

Do you remember which part of the quadratic formula is called the discriminant? Why do you think it is called this? What useful information does it give us?

How many solutions does a quadratic equation have?

How many points of intersection do the following polynomials have with the x-axis:
- y = 3 – 4x – 2x²;
- $y = \frac{1}{4}x^2 + bx + b^2$ ;
- y = 3x² – 2qx + q².

Simultaneous equations where one is quadratic

To solve, we rearrange the linear equation so that its subject is a single unknown and then substitute this unknown into the quadratic equation. As always, remember to also find the other unknown – it should be easiest to use the linear equation to do this.

Worked Example

Solve the simultaneous equations:
- x²-2xy+3y²=6; and
- 2x-3y=3.

Exercise 3

Answers

Exercise 3 Worked Solutions

Note

Sometimes at first glance it appears that an equation is not a quadratic, but then when you look a little closer you notice that actually it is. This can happen with equations like: 3a⁴ + 2a + 7 or 9a⁶ – 2a³ or $\sqrt a + 2a + 9$ .

Worked Examples

Solve x⁴+3x²-28=0
Solve x – 4√x – 12 = 0

Exercise 4

Answers

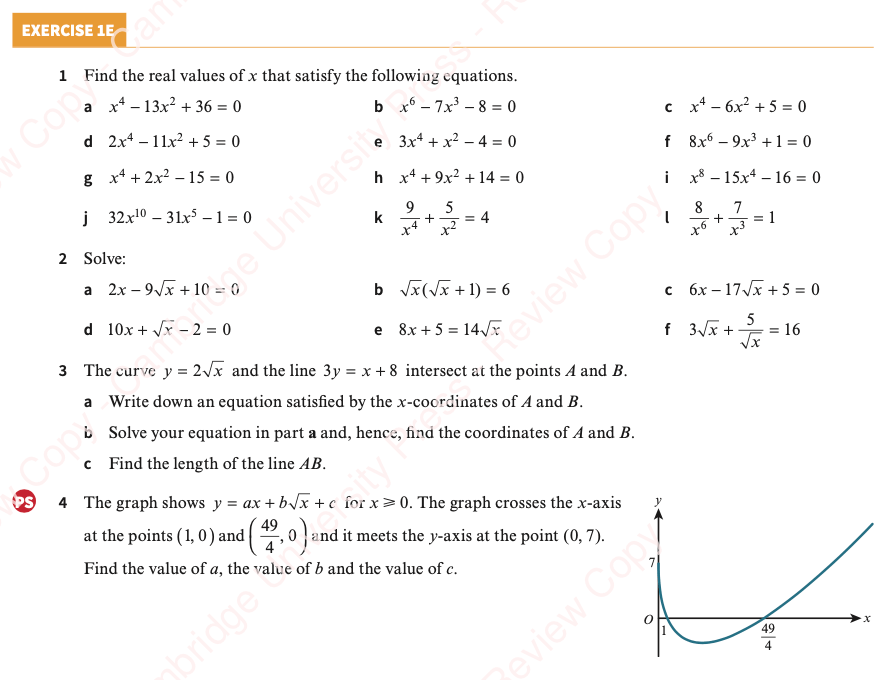
Exercise 4 Worked Solutions

Solving quadratic inequalities

When we solve a quadratic inequality, the answer is an interval rather than a specific value.

We solve them in 2 stages:

1.) We pretend the inequality is an equation to find 2 roots;

2.) We draw an upward parabola through the roots if the leading coefficient is positive or a negative parabola if it is negative. We can now identify from the graph the required interval where the y value is positive or negative. We must write this solution using set notation, making sure that we use open or closed brackets according to the question.

Worked Examples