Maths with David

    KS4. Number. Surds

    Definition of surds

    A surd is any number within a \sqrt{} sign that cannot be written without the \sqrt{} sign.

    So, what do you think, which of \sqrt{7} and \sqrt{9} is a surd and why?

    Multiplying and Dividing surds

    In general, \sqrt{x} \times \sqrt{y} = \sqrt{xy}

    and \sqrt{x} \div \sqrt{y} = \sqrt{x/y}

    So what would \sqrt{3} \times \sqrt{5} be?

    What would 3 \sqrt{2} \times 2 \sqrt{7} be?

    What would \sqrt{15} \div \sqrt{3} be?

    Adding and Subtracting surds

    It is important to recognise that adding \sqrt{x} and \sqrt{y} does not give us \sqrt{x+y}

    Instead, we notice that \sqrt{x} + \sqrt{x} = 2 \sqrt{x}

    Simplifying surds

    If we factorise a surd and notice that within the factors there is a square number, then we can simplify the surd by cancelling out this square number with the root sign.

    e.g. Simplify \sqrt{28}

    e.g. Simplify \sqrt{18}

    Exercise

    1.) Simplify the following:

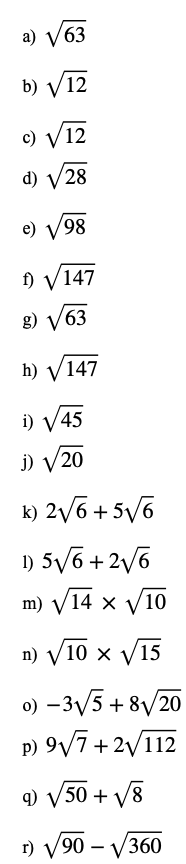
    Answers

    Rationalising a Denominator

    In general, it is seen as bad practice to have a surd in a denominator (just as we prefer not to have negative numbers in a denominator.

    It is easy to get rid of them though, using the following approach:

    \frac{x}{\sqrt{y}} = \frac{x}{\sqrt{y}} \times \frac{\sqrt{y}}{\sqrt{y}} = \frac{x \sqrt{y}}{y}

    With a fraction like this: \frac{5}{3 + \sqrt{5} } it is a little bit more difficult, but not really. We take advantage of the difference of two squares formula by multiplying the top and the bottom by 3 - \sqrt{5}

    Exercise

    1.) Rationalise the denominator:

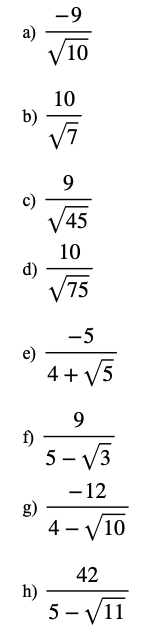
    2.) Rationalise the denominator

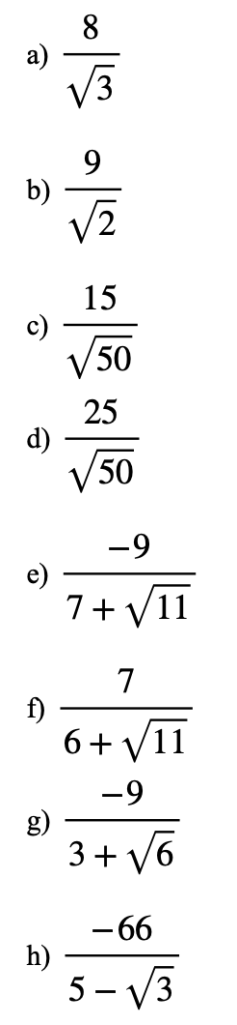
    Answers

    2.)