A bearing tells us the direction that we need to go to get from one point to another.

We always measure a bearing from North (represented by an upwards arrow on our diagrams) and measure it in a clockwise direction. We use a protractor to measure the bearing (if the bearing is greater than 180º we can use the protractor to measure the excess over 180º).

A bearing is always written using 3 digits.

Example

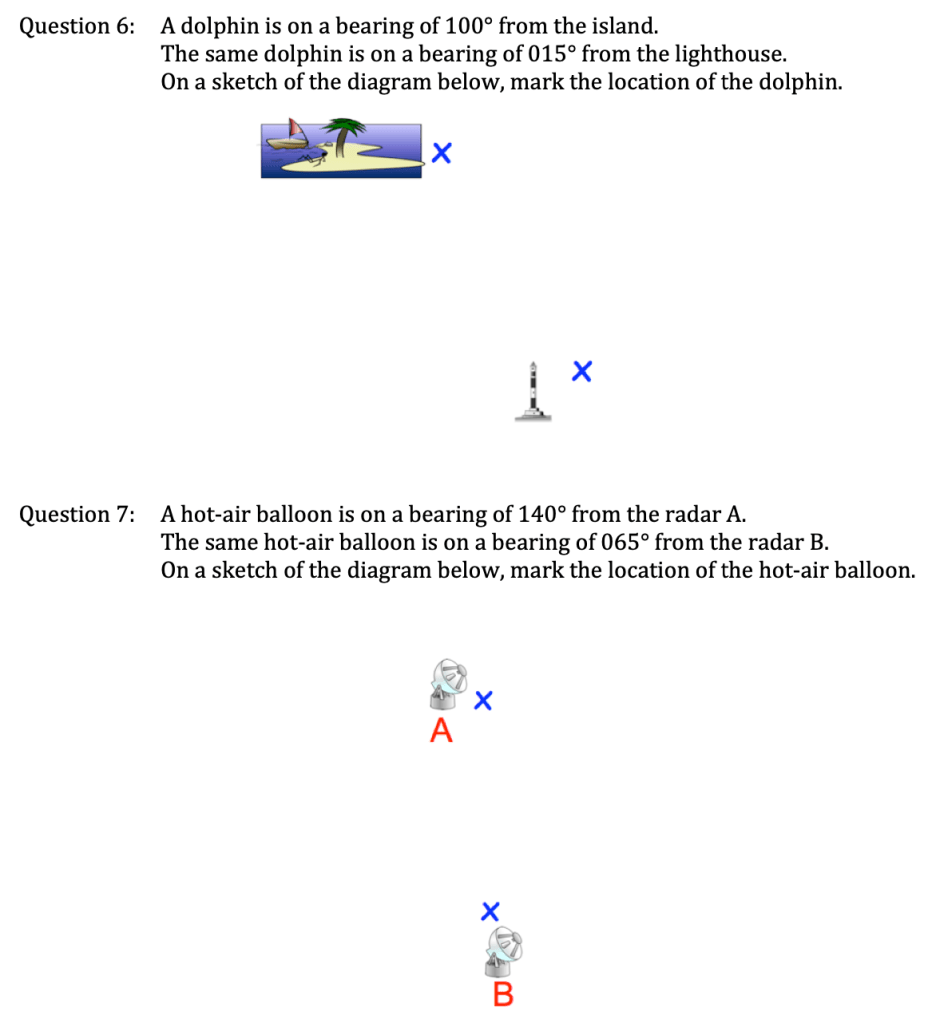
Let’s come up to the board and measure some of these bearings:

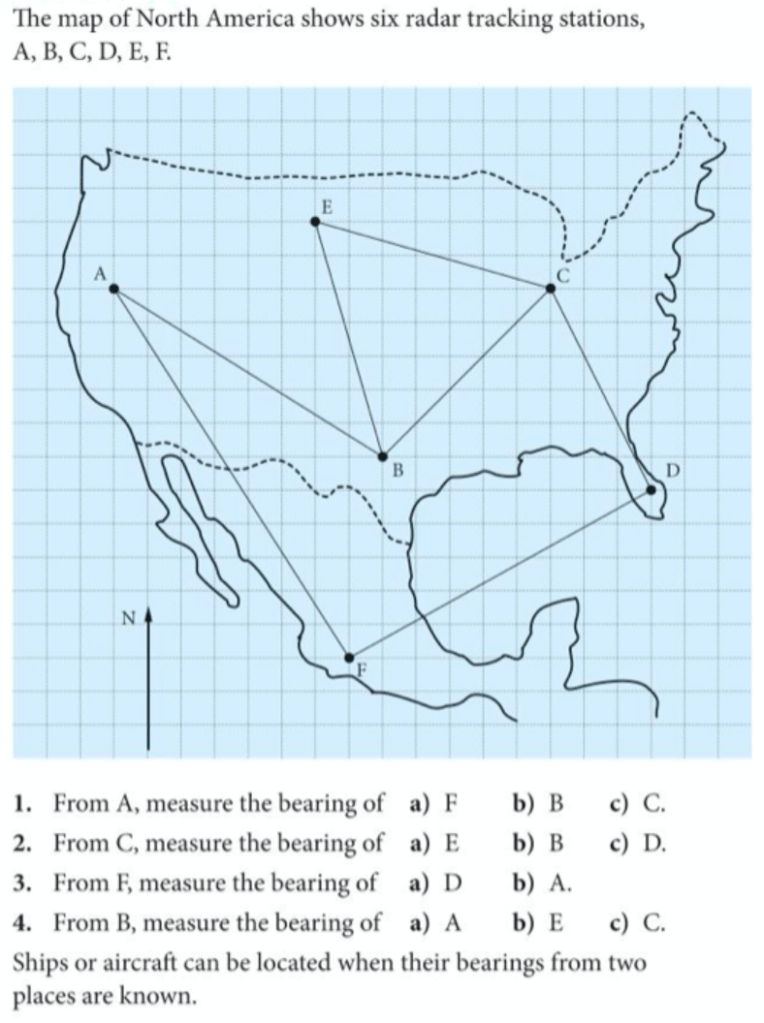
Exercises

Using accurate diagrams to calculate unknown bearings.

A motorcyclist sets off from home and travels directly east for 50km where he stops for petrol. He then travels to a cafe which is 79km from his home and at a bearing of 040º from the petrol station.

Calculate at what bearing he should set off to head directly home from the cafe.

Exercise

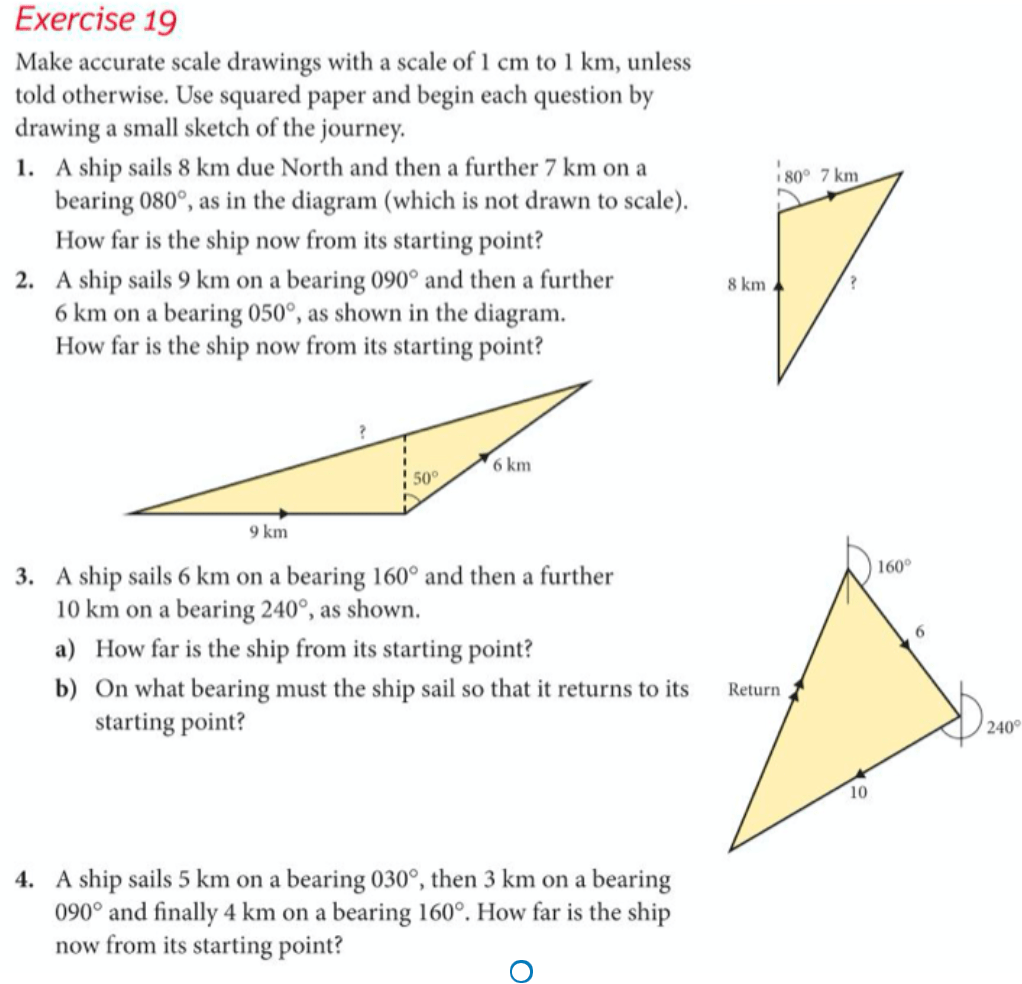
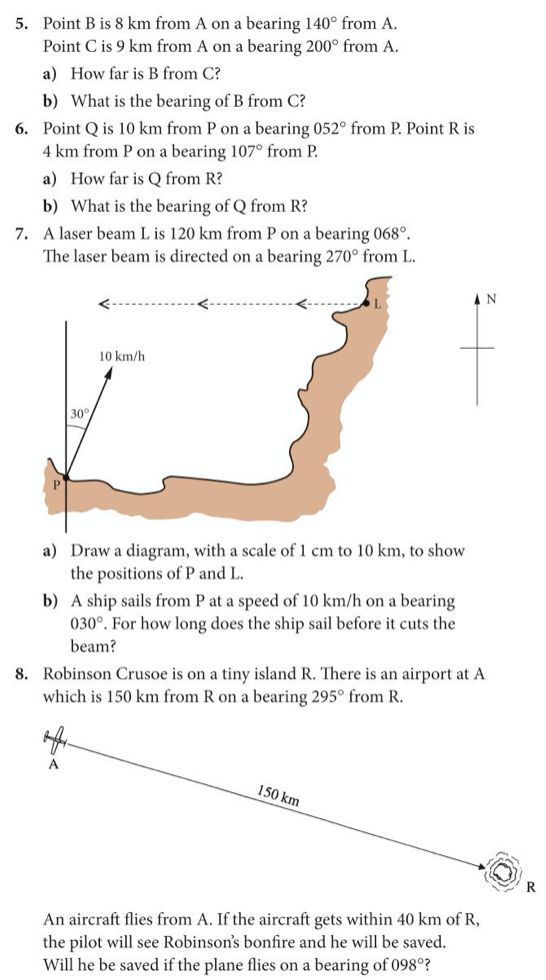
The answers, where relevant, are below:

(1.) 11.5 km; (2.) 14.1km; (3.) (a.) 12.5km (b.) 032º; (4.) 6.9km, (5.) (a) 8.5km, (b) 074º

(6.) (a) 8.4km, (b) 029º, (7.) (b) 5.2h, (8.) No

Further Practice Question

A boat sets off from a point A on a bearing of 130° for 4km to a point B.
At B it changes direction and sails on a bearing of 240° to a point C, 7km away. At point C it changes direction again and heads back to point A.
(a) Using a scale of 1cm:1km, draw a scale diagram of the boat’s journey.

(b) From your diagram work out:
(i) the distance AC ………………………………………………………………………(1 mark)

(ii) the bearing of A from C. ………………………………………………………….. (2 marks)

Answer

(b) (i) 6.8km, (ii) 026º