Although we initially define our trigonometric ratios only for right-angled triangles, we can extend this definition to define them for any angle, by drawing a unit circle on a set of axes where the horizontal axis represents cos x, the vertical angle represents sin x, and the angle anticlockwise from OX represents x. The teacher will demonstrate this and show why it means that there are infinitely many solutions to equations such as sin(x) = -1/2.

(This dynamic unit circle may help to demonstrate)

We can also generate graphs with x (i.e. the angle) along the x-axis and either sin x, cos x or tan x along the y-axis. We will look at the basics of how to do this, but you will construct the graphs as an exercise.
(This dynamic example for the sine function may help to demonstrate)

Both the unit circle and the graphs are useful for tackling trigonometric problems, including solving trigonometric equations. Let’s take a look at the questions at the bottom of the exercise with the teacher to see how this works.

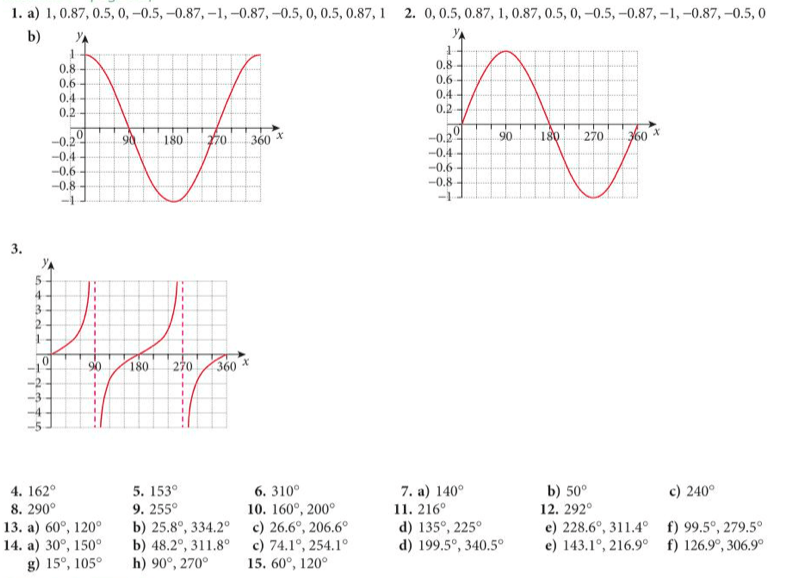
Exercise

Let’s complete some of the below exercise together and then finish it yourselves. The exercise is from page 224 of the extended textbook:

The answers are below:

Further Questions

Answers

Let’s talk a little more about using the unit circle to solve trigonometric equations (some people prefer to use the graphs – this is ok, but it is more limited). We can try with some of the questions on the following question sheet (which is followed by an answer sheet:

Solving trigonometric equations worksheet

Solving trigonometric equations answers