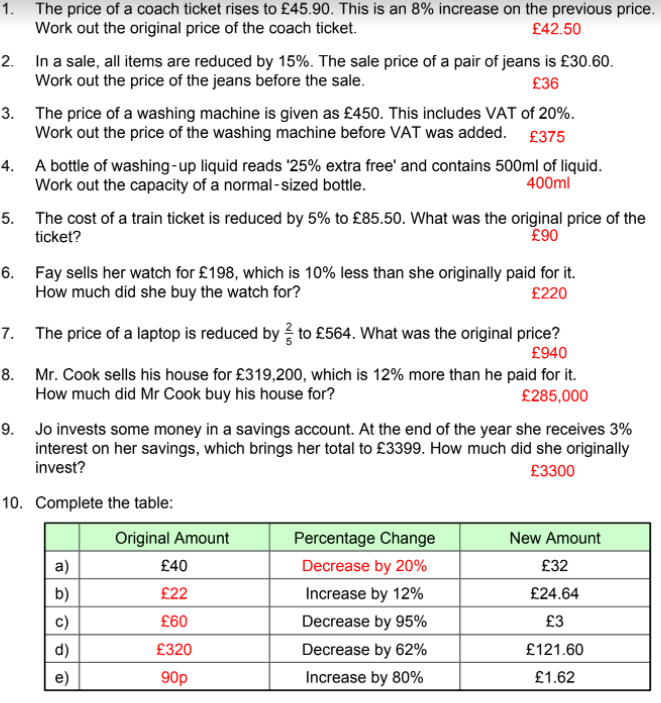
We need to be able to calculate a percentage of a quantity. To do this we just need to remember that percent means out of a hundred and that when we see the word of in mathematics we are dealing with a multiplication. Let’s practice some:

Examples (Let’s not use a calculator on the first ones)

Exercise

Odd numbered questions should be done without a calculator. On even numbered questions, you can use a calculator (rounding your answers to the nearest penny):

• (1.) 20% of £60, (2.) 4.5% of £6.22, (3.) 10% of £80, (4.) 17% of £6.84
• (5.) 5% of £200, (6.) 15% of £8.11, (7.) 6% of £50, (8.) 17% of £17.07,
• (9.) 4% of £60, (10,) 37% of £9.64 (11.) 30% of £80, (12,) 3.5% of £12.90,
• (13.) 9% of £500, (14.) 8% of £11.64 (15.) 18% of £400, (16.) 68% of £54.45,
• (17.) 61% of £400, (18.) 73% of £23.24 (19.) 12% of £80, (20.) 2.5% of £15.20,
• (21.) 6% of £700, (22.) 6.3% of £12.50, (23.) 11% of £800, (24.) 8.2% of £19.50
• (25.) 5% of 160kg, (26.) 87% of £15.40, (27.) 20% of 60kg, (28.) 80% of £62.50,
• (29.) 68% of 400g, (30.) 12% of £24.50, (31.) 15% of 300m, (32.) 12.5% of £88.50,
• (33.) 2% of 2000km, (34.) 7.5% of £16.40 (35.) 71% of £1000, (36.) 5.5% of £80,
• (37.) 26% of 19kg, (38.) 12.5% of £90, (39.) 1% of 6000g, (40.) 19% of £119.50
• (41.) 8.5% of £400, (42.) 8.35% of £110.

Answers

(1.) £12, (2.) 28p (3.) £8, (4.) £1.16, (5.) £10, (6.) £1.22, (7.) £3, (8.) £2.90, (9.) £2.40, (10.) £3.57, (11.) £24, (12.) 45p, (13.) £45, (14.) 93p (15.) £72, (16.) £37.03 (17.) £244, (18.) £16.97, (19.) £9.60, (20.) 38p (21.) £42, (22.) 79p, (23.) £88, (24.) £1.60 (25.) 8kg, (26.) £13.40 (27.) 12kg, (28.) £50, (29.) 272g, (30.) £2.94 (31.) 45m, (32.) £11.06 (33.) 40km, (34.) £1.23, (35.) £710, (36.) £4.40 (37.) 4.94kg, (38.) £11.25, (39.) 60g, (40.) £22.71, (41.) $204, (42.) £9.19.

Percentage change

If we want to increase an amount by a fixed percentage (or decrease an amount by a fixed percentage), it is easiest to add (or subtract) that percentage to 100% (which represents the original amount), and then just multiply by this new number.

Example

A £260 television has a premium version which is 20% more expensive than the regular version. How much does it cost?

The basic version doesn’t sell well in the first few months, so its price is decreased by 20%, how much does it now sell for?

If a 17.5% sales tax is levied on both of the versions of the television (i.e. the premium version and the discounted original version), then how much will the total sales price be?

Exercise

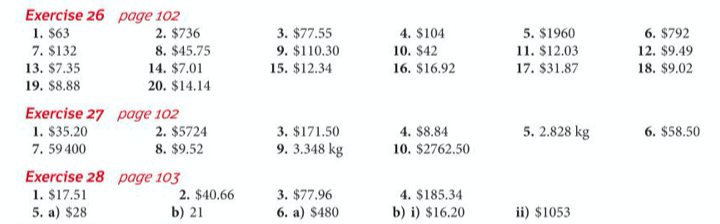
After practicing using this approach to calculate a new quantity after a percentage change, we will apply this skill to word problems, and then deal with more involved problems where we apply tax to a bill. Let’s complete exercises 26, 27 and 28 from pages 102 to 104 of the core textbook:

The answers are below:

Reverse percentages

If a product has a price increase of 20% and the price after this increase is 120, then we know that the original price must have been £100. Note that we do not calculate this by reducing the £120 by 20% (which would give us £96). This is an example of a reverse percentage. Below are two examples of how these are tackled:

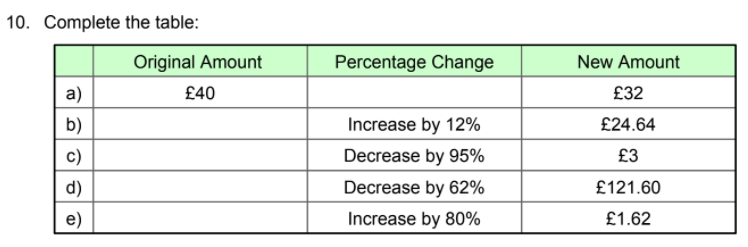
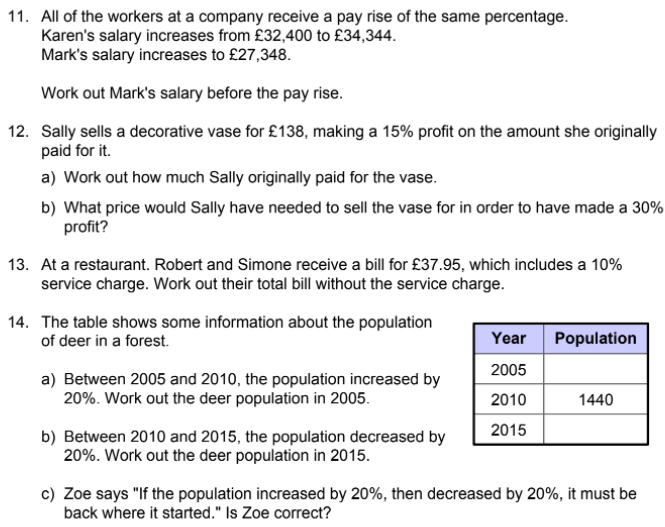
Exercise

Answers