Quadratic Expressions

A quadratic expression is any expression whose highest power is 2, for instance 3x²+4x+9 or 1-7x².

These expressions and the related equations are very important and are the most difficult type of equations we tackle in our iGCSE course. So we will spend some time getting to know them and look at various different methods for solving them.

First, we are going to learn to factorise them.

To introduce this we will start by looking at expressions of the form x²+bx+c (that means ones where the x2 term does not have a coefficient).

To factorise these expression we must find two numbers whose product is c and whose sum is b. One or both of these numbers could be negative. Let’s see what we mean:

Factorise:

• x² + 6x + 8
• x² + 2x – 15
• x² – 6x + 8

Let’s come up to the board and factorise some:

x2 – 9x + 8	x2 + 24x + 23	x2 – 5x – 14	x2 – 7x + 12
x2 + 12x + 36	x2 – 2x – 63	x2 + 14x + 24	x2 + 17x + 60
x2 – 11x + 30	x2 – 4x – 32	x2 +18x + 56	x2 – 16x – 17
x2 – 11x + 18	x2 – 13x + 22		x2 – 21x + 110

Exercise

Before we move to more complicated situations, let’s practice this technique, as we are going to use it a lot. The exercise is exercise 25 from page 86 of the extended textbook:

The answers are below:

1. (x+2)(x+5)
2. (x+3)(x+4)
3. (x+3)(x+5)
4. (x+3)(x+7)
5. (x+2)(x+6)
6. (y+5)(y+7)
7. (y+3)(y+8)
8. (y+5)(y+5)
9. (y+3)(y+12)
10. (a+2)(a-5)
11. (a+3)(a-4)
12. (z+3)(z-2)
13. (x+5)(x-7)
14. (x+3)(x-8)
15. (x-2)(x-4)
16. (y-2)(y-3)
17. (x-3)(x-5)
18. (a+2)(a-3)
19. (a+5)(a+9)
20. (b+3)(b-7)
21. (x-4)(x-4)
22. (y+1)(y+1)
23. (y-7)(y+4)
24. (x-5)(x+4)
25. (x-20)(x+12)
26. (x-15)(x-11)
27. (y+12)(y-9)
28. (x-7)(x+7)
29. (x-3)(x+3)
30. (x-4)(x+4)

Quadratic Expressions with a Coefficient of x²

Now let’s complicate the situation a little, by instead of only looking at expressions of the form x²+bx+c, looking at more general expressions of the form ax²+bx+c.

Here we have two stages. Let’s see these stages for a concrete example. As this process is a little more involved, it is worth copying this example down in our book so we can refer to it:

Factorise 3x²+13x+4:

• Find two numbers whose product is 12 (because 3×4=12) and whose sum is 13. In this case the numbers are 1 and 2;
• Split the 13x term based on these two numbers: 3x²+x+12x+4;
• Factorise in pairs: x(3x+1) + 4(3x+1);
• (3x+1) is a common factor: (3x+1)(x+4).

Examples – Teacher can do first few then let’s come to the board!

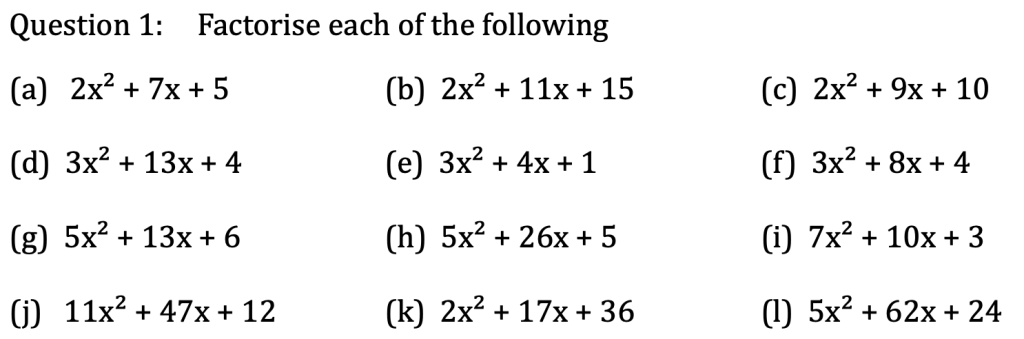
Exercise

Now we should be able to complete exercise 26 from page 86 of the extended textbook:

The answers are below:

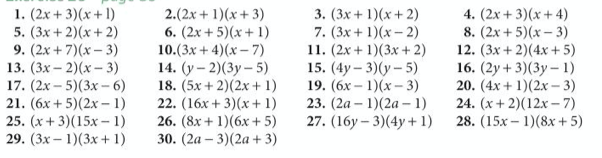
Quadratic Equations

Now that we’ve dealt with factorising quadratic expressions, we can start to solve quadratic equations. As long as the right hand side of the equation is zero, this is simply a case of factoring the left hand side, then identifying the solution from each of the factors.

Example

Exercise

Let’s complete exercise 28 on page 88 of the extended textbook:

The answers are below:

Quadratic Formula

What we have learned above is great, if we can identify the integer factors. But sometimes we can’t. Thankfully, by doing a little algebraic manipulation to the equation ax²+bx+c=0, we can derive a formula which we can then just use every time to calculate our solutions. So let’s do that.

Example

Exercise

Let’s complete exercise 30 from page 90 of the extended textbook:

The answers are below:

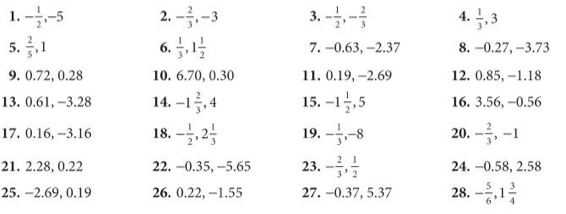
Completing the Square Technique

This is a more advanced technique that can help us solve quadratic equations without using the formula. Let’s see the technique for x²-6x+7=0

Examples

Exercise

Let’s complete exercise 32 on page 93 of the extended textbook:

The answers are below:

Now let’s try using our knowledge of how to solve quadratic equations to solve some “word problems”, by completing exercise 33 on pages 95 to 96 of the extended textbook:

The answers are below: