An inequality is a bit like an equation, but instead of an equals sign we have a “crocodile” to show us which side of the inequality is the largest.

So let’s try writing the appropriate crocodile between the following pairs of numbers:

2 7

-2 -5

π 3

9² 80

7/15 3/5

When we talk about solving an inequality, it is similar to solving an equation because we want the letter on its own. The algebraic manipulation that we are allowed to do with inequalities is almost exactly the same as with equations except that we have to be careful if we multiply or divide by a negative number, because this will change the direction of the crocodile.

Example: Solve x – 4 > 7. Solve 2x+3 < 9 Solve 4 – x > 10 Solve 3x – 7 < 2x + 9

Exercise

Let’s complete exercise 15 on page 194 of the extended textbook:

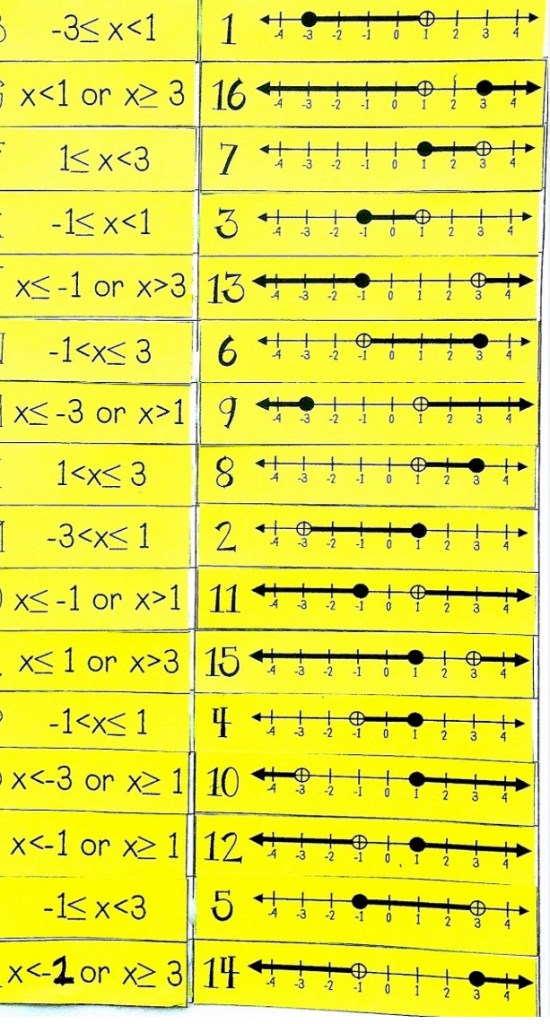
The answers are below:

Number lines

A number line can be a great way to show the solution to an inequality. If the inequality is strict, we draw an open circle at the end of our line. If the inequality is non strict we draw a closed circle at the end of our line.

Example

An alternative way to show solutions, particularly good if the solutions are all integers is to use set notation to show our answer, e.g. {2, 3, 4, 5, 6}

Exercise

Let’s complete exercise 16 from pages 195 and 196 of the textbook:

The answers are below:

“Compound” or “double” Inequalities

An inequality can have more than one crocodile. In this case it is best to consider each crocodile separately and solve as we have done previously, to find the interval for which both of the inequalities hold true.

Examples

Exercise

For each of the questions below, express the solution as an inequality (i.e. using crocodiles), and then draw a number line to represent the solution.

Answers