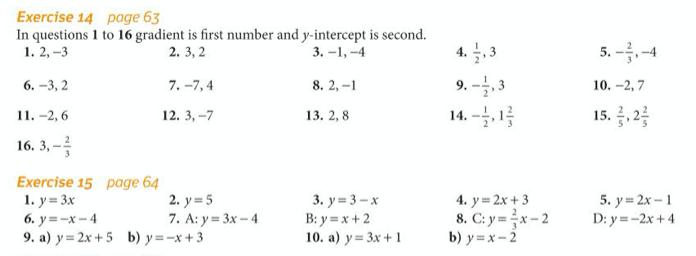Let’s focus again on graphs which are straight lines. These don’t have powers of x in, so look something like y = 3x – 2, of 3y = 1 – x.

One of the most important properties of a straight line graph is its gradient. This tells us how steep it is. If the gradient is 0, the line is horizontal. If it is 1 it is at a 45º angle. If it is -1 it goes down at a 45º angle. What about other gradients?

If we know two points on the line, we can easily find the gradient. We simply take the difference between the y-coordinates and divide that by the difference between the x-coordinates.

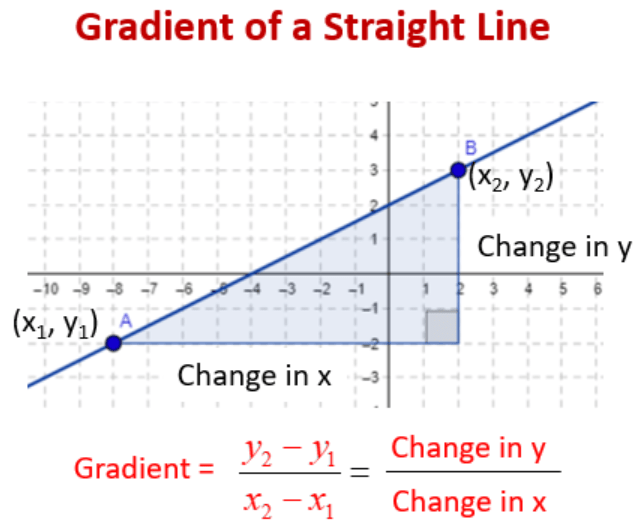
Let’s try finding some gradients with the teacher.

Exercise

Let’s complete exercise 12 from page 61 of the core textbook:

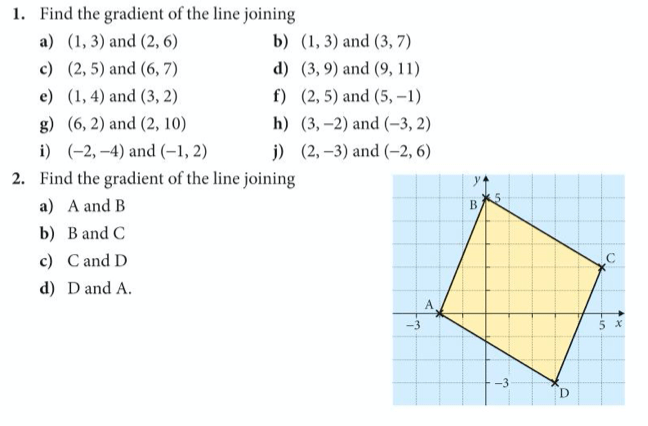
The answers are below:

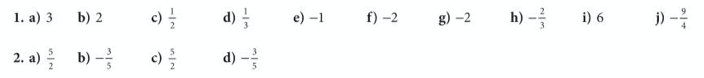
y-intercept

The y-intercept is the y-coordinate at which a line crosses the y-axis. So if it crosses at (0,4) then the y-intercept is 4.

If we know the gradient and the y-intercept of a line, it should be easy to draw it on cartesian axes. Let’s try some.

Exercise

Let’s complete exercise 13 from page 62 of the core textbook:

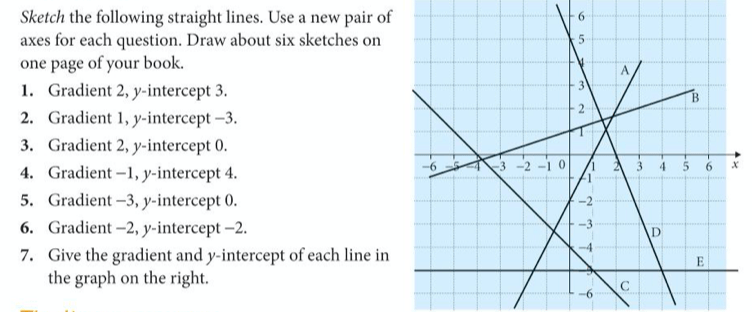
The answers are below:

y=mx+c form of straight line equation

We often like to use algebraic manipulation when we have an equation of a straight line to put it into the form y=mx+c. This form is useful to us, because it tells us the gradient of the line, m, and the y-intercept. So we can draw the line. Let’s try manipulating some equations into this form and then drawing them.

Exercise

Let’s complete exercises 14 and 15 from pages 63 to 65 of the core textbook:

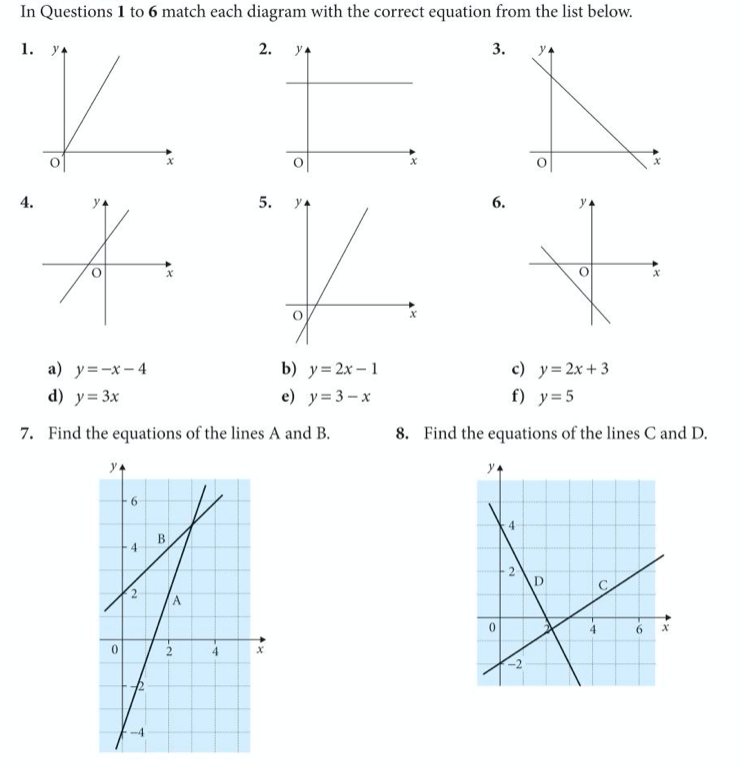
The answers are below: