In English we call simultaneous equations what in Russia are called a system of equations. This is where we have more than one equation that is true at the same time. For example:

• y=2x
• y=x+1

In this situation, to solve the equations, we need to find out both of the unknown values. So our answer should say the value of x and the value of y.

There are three different methods that we need to know. Even if one is our favourite, we must learn all three and examinations may ask us to use a specific one. This is because certain methods work better for certain simultaneous equations and certain methods work better for others.

The three methods that we will look at are:

• (1.) Solving graphically;
• (2.) Solving algebraically by substitution; and
• (3.) Solving algebraically by elimination.

1. Solving Graphically

The idea of this method is that we draw the line (or curve) represented by each of the equations, and where the two lines (or curves) intersect, this gives us the solution (the x-value and y-value) to our equation. As always when we represent an equation on a graph, the x-value is represented by distance along a horizontal axis and the y-value is represented by distance along the vertical axis.

So let’s try using this method to solve the system of equations that we discussed above:

• y=2x
• y=x+1.

Practice with teacher

Here are some more examples so that we can practice some of them together:

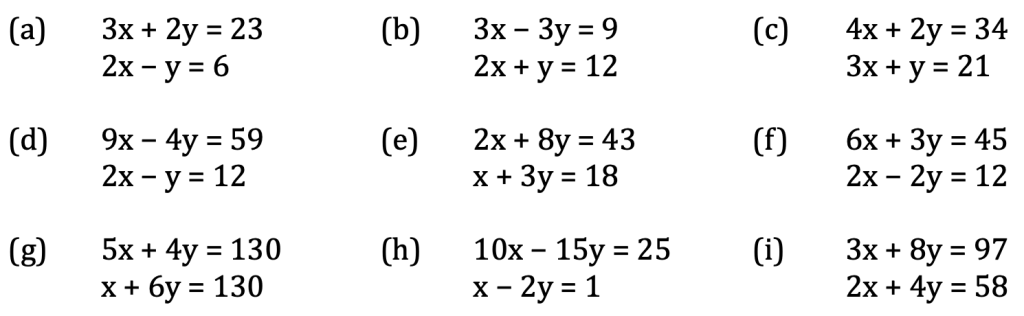
Exercise

Now let’s try exercise 4 on pages 227 to 228 of the core textbook:

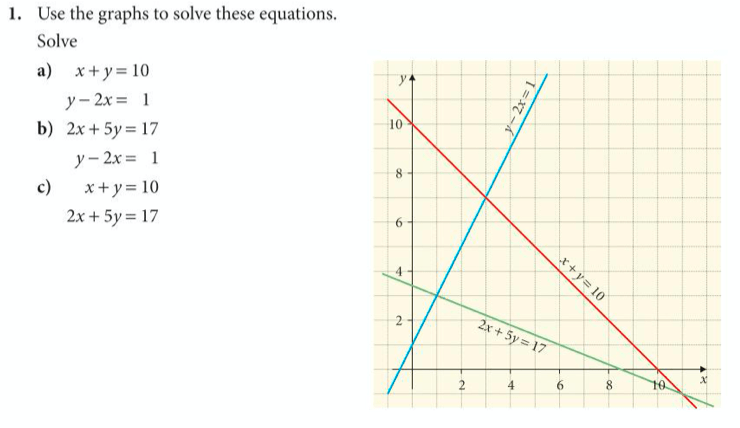
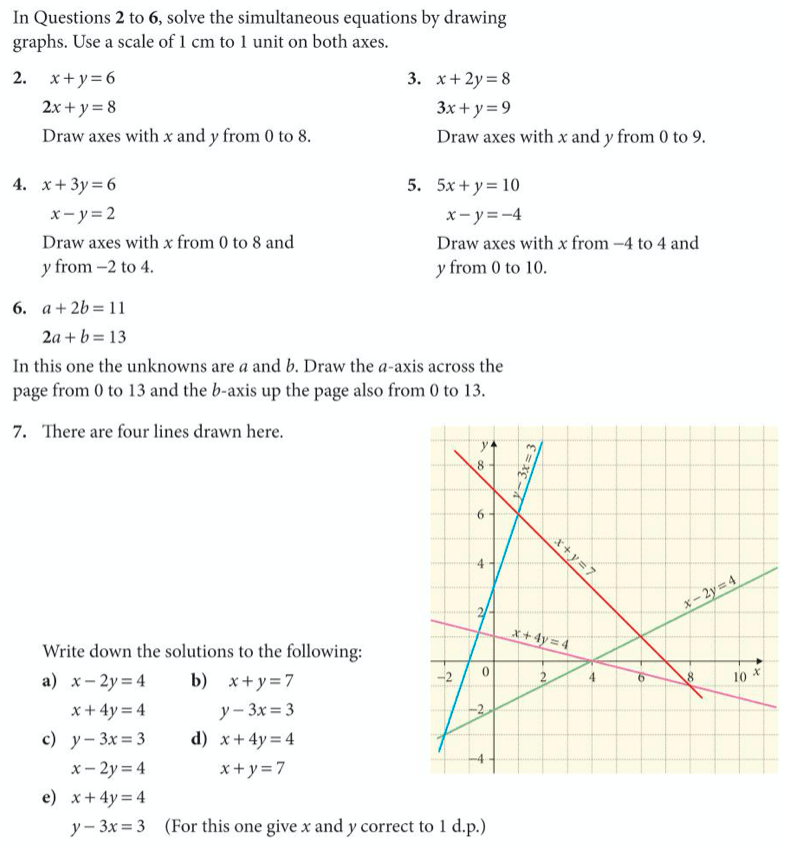
The answers are below:

2. Solving algebraically by substitution

Drawing a graph is generally quite a time-consuming way of solving an equation, and in practice we only really use it if the graph is too complicated for us to handle algebraically. We do need to know the method though, so that we are prepared in the future for that kind of situation.

Solving algebraically is more straightforward and follows are normal methods of algebra. Let’s try solving our above equations by substitution:

• y=2x
• y=x+1.

We can also practice this method with the examples towards the top of this page.

Exercise

Let’s practice this method in exercise 5 on page 229 of the core textbook:

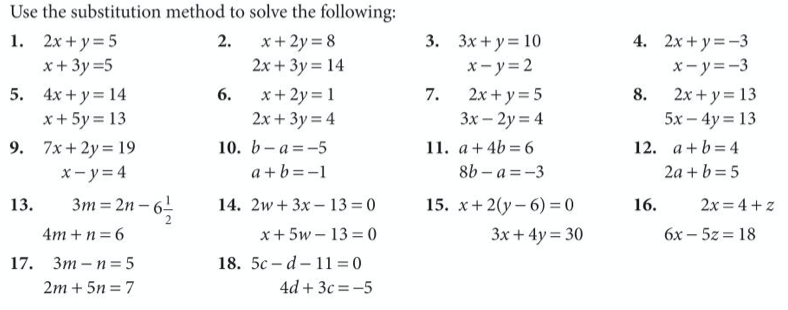
The answers are below:

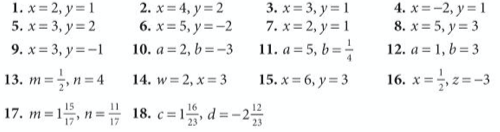
3. Solving algebraically by elimination

A lot of people find the “elimination” method the easiest to use. In this we add or subtract together our equations (or multiples of our equations) in order to eliminate one of the variables. Let’s try it with the example that we’ve been using so far:

• y=2x
• y=x+1.

We can also practice this method with the examples towards the top of this page.

Exercise

Now let’s practice this method of solving simultaneous equations in exercise 6 on page 230 of the core textbook:

The answers are below:

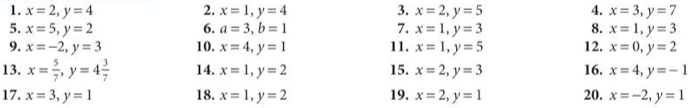
Solving problems using simultaneous equations

Let’s try using our new skills with simultaneous equations to solve a variety of word problems

Examples

Exercise

We will complete exercise 7 on pages 231 to 232 of the core textbook:

The answers are below:

Extension work

Below are some further questions to practice applying our skills with simultaneous equations from exercise 22 on pages 82 to 84 of the extended textbook:

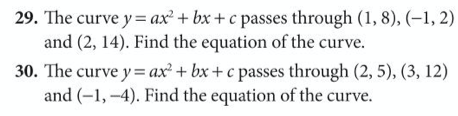
You can find the answers below: