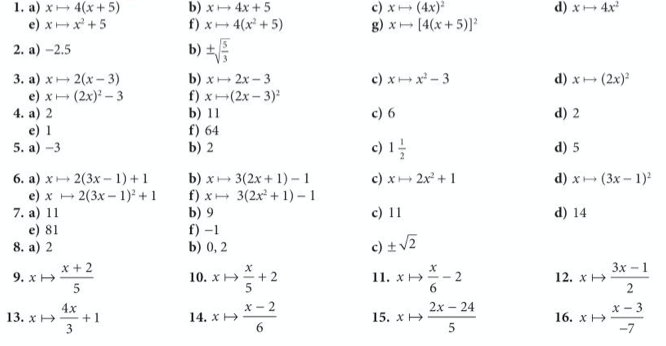You have already met the concept of functions in algebra.

A function is a rule that takes a set of inputs and terms it into a set of outputs.

For instance, the function f(x)=2x+1 takes the value 1 and turns it into 3. It takes the value 2 and turns it into 5. What does it do to the value 3?

In a function f(x), x is called the argument of the function. This is where the input values go.

We can write a function as f(x)=2x+1 or as f:x |-> 2x+1. Both mean the same thing. And if we want to refer to the value when the input is 2, we would write f(2). (So f(2)=5).

If we know the output value of a function we can work backwards (e.g. if f(7)=9, then 2x+1=9, so x=4).

Exercise

Let’s complete exercise 11 on pages 305 to 307 of the extended textbook:

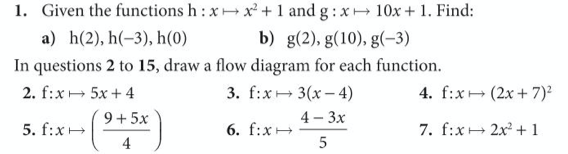
The answers are below:

Composite functions and Inverse functions

f(g(x)) is a composite function, where we apply g(x) first and then f(x) second. Let’s see what this means in practice for a few functions and arguments, and then let’s think what f(f(x)) means.

If we want to find the inverse of a function, we follow a simple method which involved switching the variables and then changing the variable that is the subject of the equation. Let’s practice this with the teacher.

Exercise

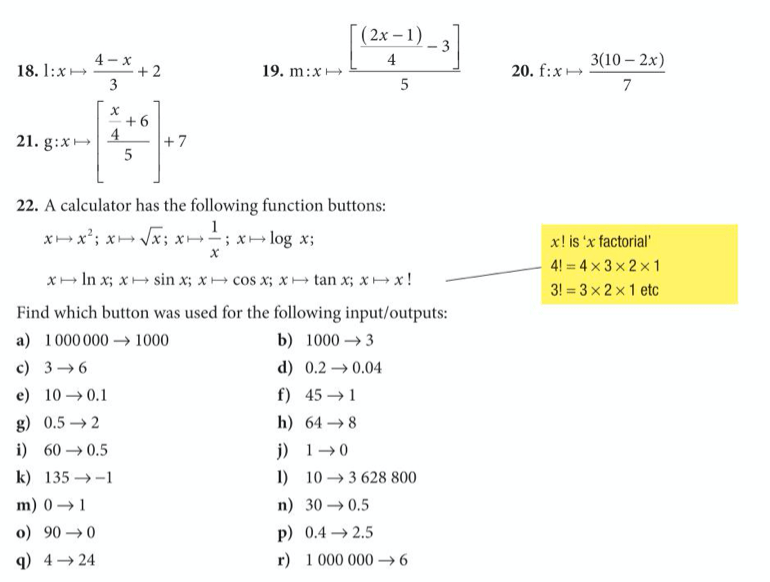
Let’s complete exercise 12 from pages 308 to 310 of the extended textbook:

The answers are below: