We have already looked at sequences earlier in the year. Now we want to focus more carefully on how to find the nth term of different sequences. The nth term is a rule that let’s us calculate the value of a specific term of the sequence, given its position in the sequence (e.g. the 213th term in the sequence).
Linear sequences
A linear sequence (also known as an arithmetic sequence) is one where each term in the sequence is a fixed amount larger than the previous term. eg. 10, 13, 16, 19, 22, … is a linear sequence.
For this kind of sequence we can use a special technique to calculate the nth term of the sequence.
This technique is illustrated below:

Let’s try this together for a few sequences from the following:

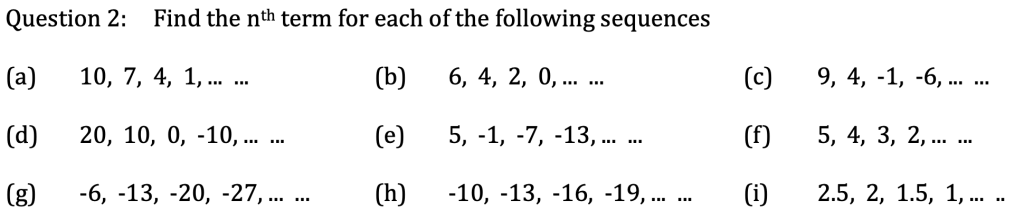
Linear Sequences Exercise










Answers









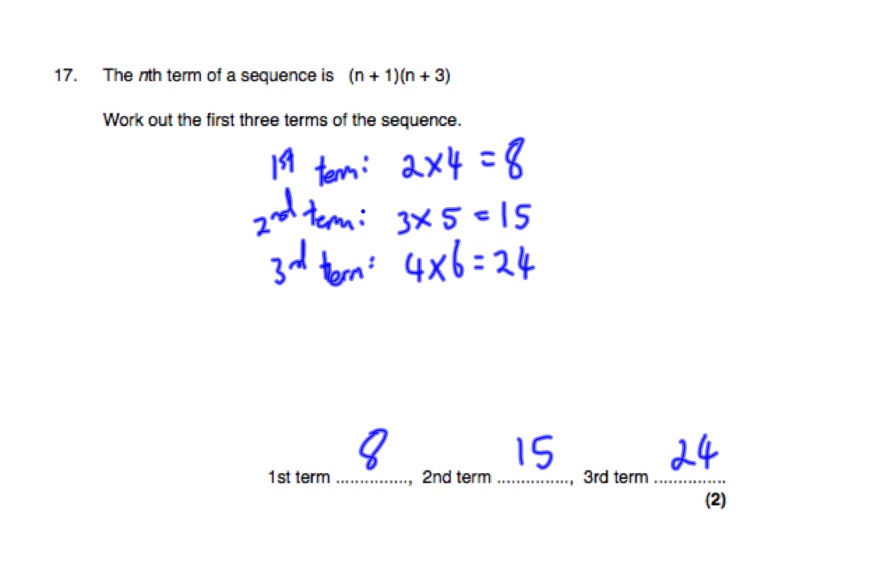
Quadratic Sequences
Finding the nth term with quadratic sequences follows a similar process.
In this case, if we identify that the “second difference” between the terms of the sequence is quadratic, then we know it must be a quadratic sequence with the form , so our job is to use the first, second and third term to identify the coefficients a, b and c for our specific sequence.









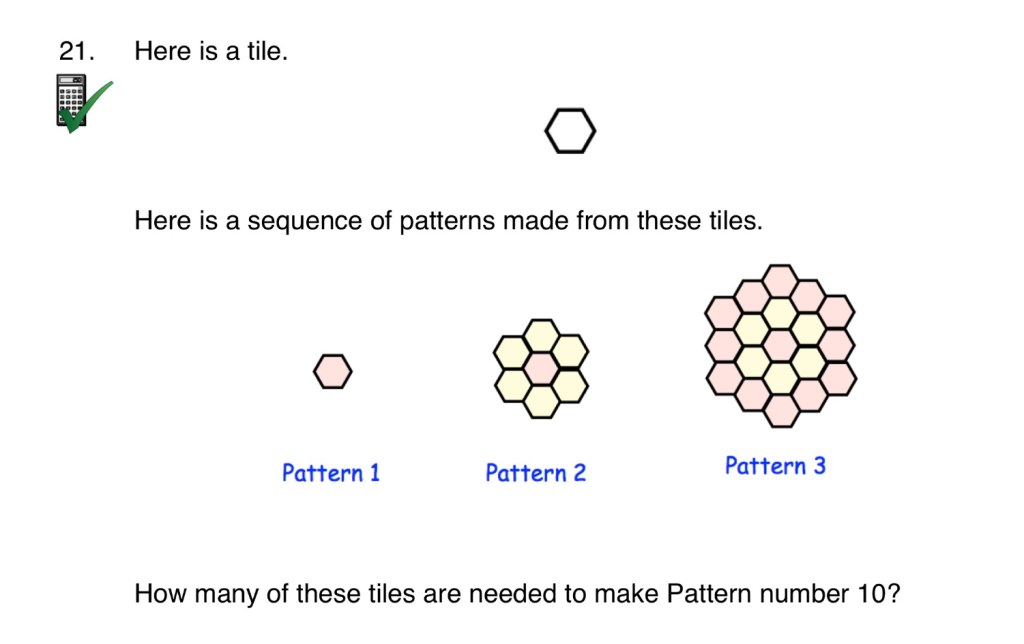

Answers







