Changing the subject of a formula is like a game where our aim is to rewrite an equation in our preferred way.

So, for instance, we might have the formula and want to rewrite it as ” u = something”. This is called “making u the subject of the formula“.

So, how would we do it? Well there is only one rule. We can do any arithmetical operations we want to, but we must always do exactly the same to both sides of the equation. Let’s do it now to make u the subject of the equation.

Making t the subject of the equation is a little bit more difficult. Let’s try it!

Worked Examples

Make x the subject of the following formulae:

First set of exercises

Let’s complete exercises 13, 14 and 15 from the textbook:

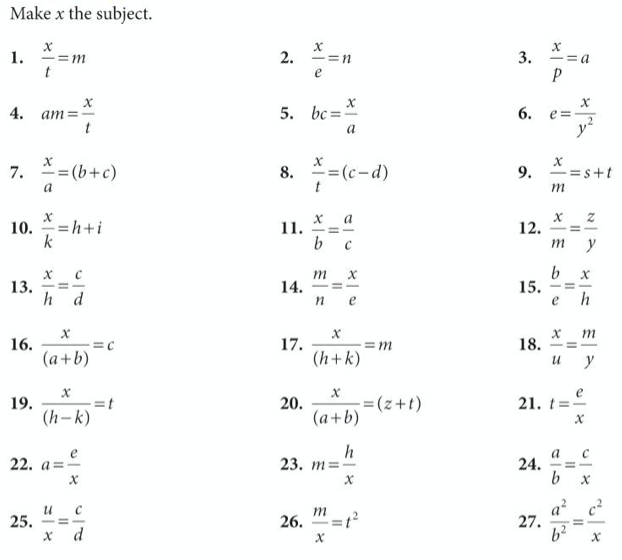
The answers are below:

(1.) x = e-b, (2.) x = m+t, (3.) x = a+b+f, (4.) x = A + B – h, (5.) x = y

(6.) x = b-1, (7.) x = m-k, (8.) x = w+y-v, (9.) x = b/a, (10.) x = m/h

(11.) , (12.) , (13.)

(14.) , (15.) , (16.)

(17.) (18.) (19.)

(20.) (21.) (22.)

(23.) , (24.) (see 25-30 below)

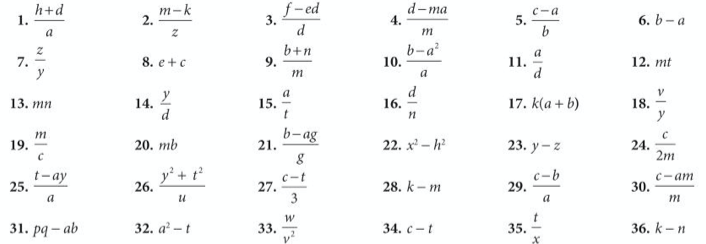
Further, progressively more advanced exercises

• Second set of exercises;
• Third set of exercises (Variable on denominator);
• Fourth set of exercises (Involving squares and roots); and
• Fifth set of exercise (Requiring factorisation).