With all fractions, we prefer to write them in simplest form, also called their lowest terms. We do this by dividing the numerator and the denominator by any common factors they have. We must always divide them both by the same thing.

Worked Examples

• Simplify the following algebraic fractions:
  • a.
  • b.
  • c.
  • d.
  • e.
  • f.
  • g.
  • h.

Exercise

Let’s complete exercise 1 from page 174 of the extended textbook:

The answers are below:

Algebraic Fractions including Quadratic Expressions

Now we will start to look at more difficult examples, for instance involving quadratic expressions.

Note that in order to simplify algebraic fractions, we may need to factorise them first using techniques we have already learned:

Worked Examples:

• Simplify the following algebraic fractions:
  • a.
  • b.
  • c.
  • d.
  • e.
  • f.
  • g.
  • h.
  • i.
  • j.
  • k.
  • l.
  • m.

Exercise

Let’s complete exercise 2 from pages 174-175 of the extended textbook:

The answers are below:

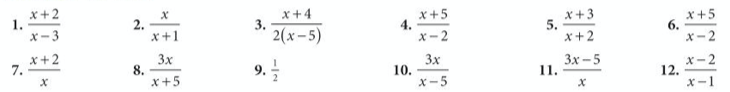
To add or subtract fractions together, we always need the denominators to be the same. This is the case whether the fractions are numerical or algebraically. To get the denominators the same, we can multiply either of the fractions through by anything we need to, as long as we remember that whatever we multiply the denominator by we must also multiply the numerator by. The most straightforward way to do it is by ensuring the denominators of the fractions both show the lowest common denominator of their original denominators.

Example

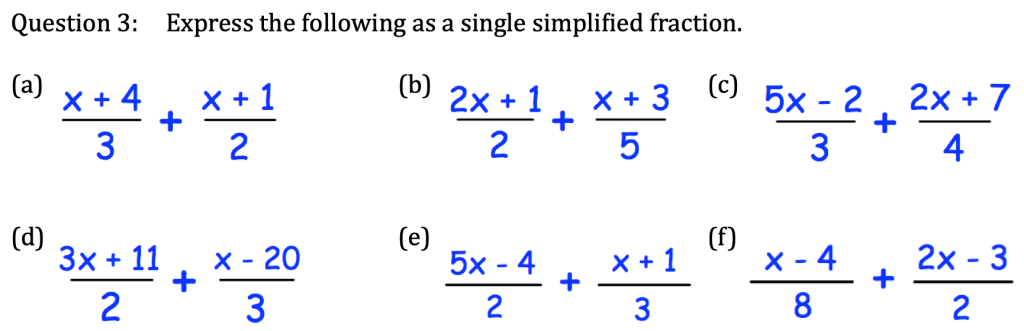
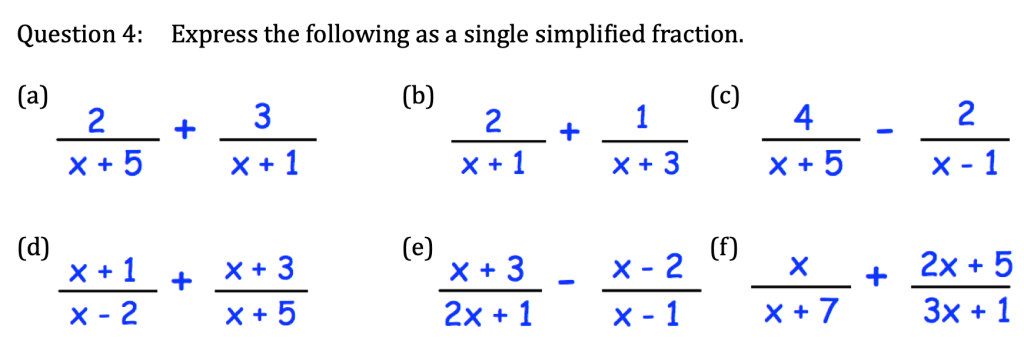
Exercise

Let’s complete exercise 3 from pages 175 to 176 of the extended textbook:

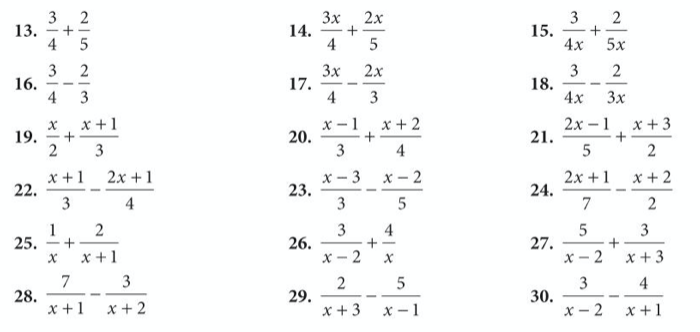
The answers are below: