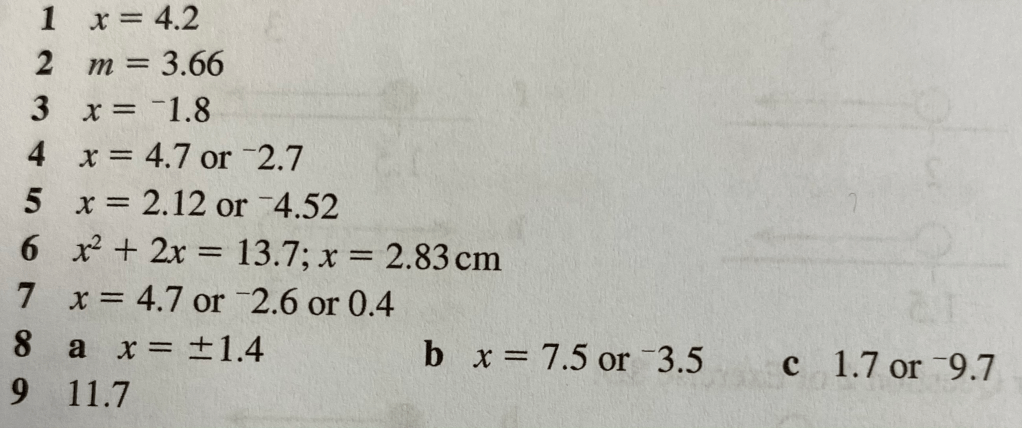Quadratic equations are more complicated equations, where as well as having an unknown value (a letter), the equation includes the square of an unknown value (e.g. x²). Solving them is a little more difficult. We will learn how to do it later this year, but for now we are going to approximately solve them using trial and improvement.

The trial and improvement method we use is to try a value for “x”. If the result is too large we try a smaller value and if the result is too small we try a larger value. Carrying on like this we can calculate the value to whatever degree of accuracy we require. (Although this may seem like a kind of guessing, it is actually part of a very important topic within mathematics that is studied at university and beyond, know as numerical analysis).

Example

Before doing the exercise below, let’s try finding the value of x to a fixed number of decimal places when x²=10 or x²=20.

Exercise

Let’s complete exercise 8G on page 121 of the textbook:

The answers are given below: