When we talk about congruence, we are interested in a shape, regardless of its position or if it has been rotated. So two shapes are congruent if they are the same in every way, except for their position or if they have been rotated.

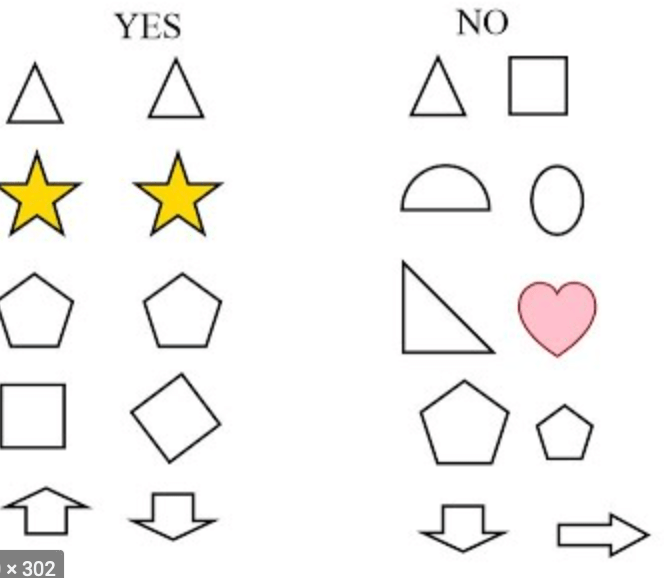
When shapes are congruent, they will have corresponding vertices and corresponding sides. These are the ones with “fit on top of each other”.

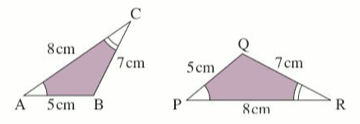
So what are the corresponding vertices to A, B and C above? And what are the corresponding sides to AB, AC and BC?

Exercise

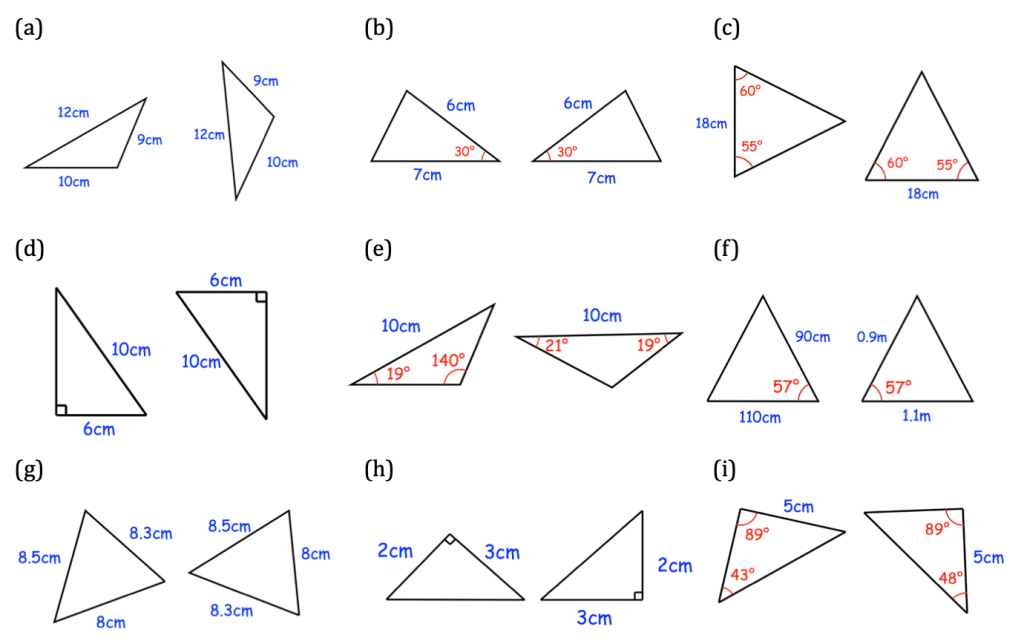
Let’s complete exercise 3E on pages 43 and 44 of the textbook (you will need the physical copy of the book to do this):

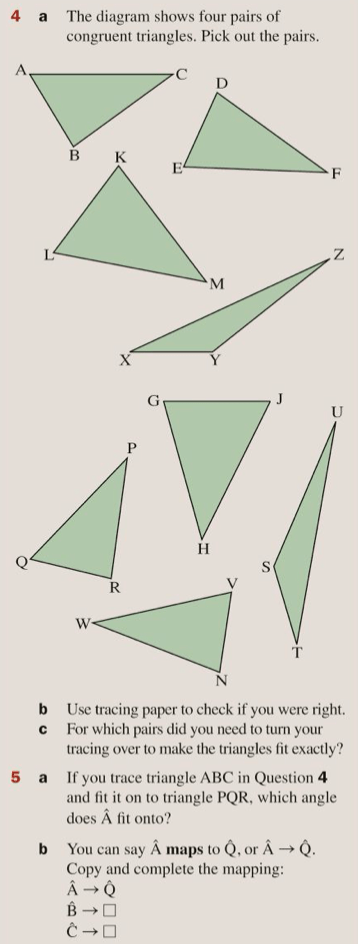
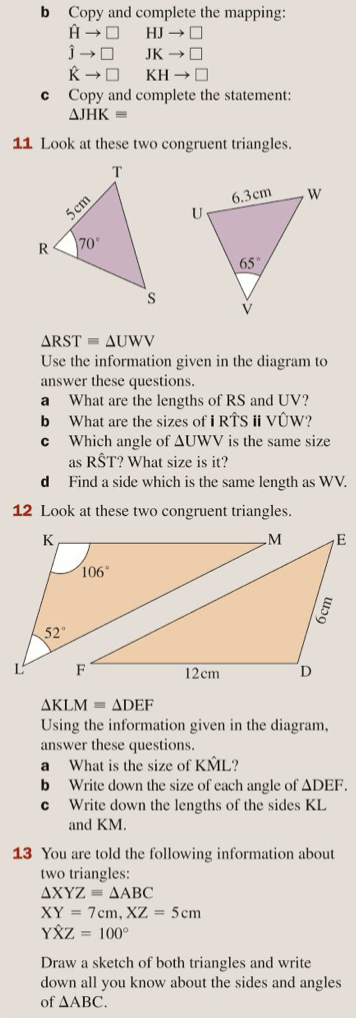
The answers are below:

If we know that a shape is congruent, then we know that the corresponding sides have equal length. But how do we know that two triangles are congruent? They are congruent if they pass one of the following congruency tests:

• SAS;
• AAS;
• SSS;
• RHS.

Once we know that they are congruent, we know that the corresponding angles are equal in size and that the corresponding lengths are equal in size.

Let’s try the following exercise:

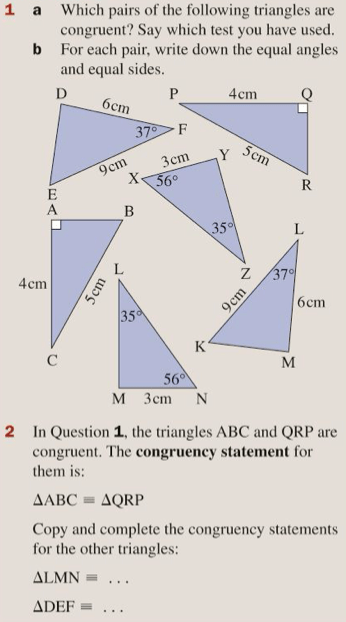
Exercise

Let’s complete exercise 3F on pages 45 and 46 of the textbook:

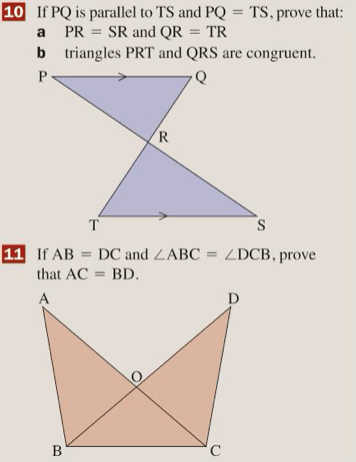
The answers are below: