Vector Geometry is a whole branch of geometry, and a very useful one. Indeed, it was the language that Einstein used when he wrote his groundbreaking Theory of Special Relativity and Theory of General Relativity. Without those theories, GPS (the Global Positioning System) would not be possible, which would mean that there would be no Yandex Maps or Google Maps to help you find where you were in a city, or to order a taxi!

It is basically an extension of Cartesian Geometry, in which we remove the axis and use vectors to specify position in space relative to a fixed point (the origin) and movements in space.

We write vectors as a column of two numbers, the top number showing how far to the right we have moved and the bottom number showing how far up we have moved:

Example

Adding and subtracting vectors

Adding and subtracting vectors is intuitively straightforward. To add two vectors we just take a new vector that has the combined effect of the two vectors given. Subtraction is the same, except that the vector subtracted goes in the opposite direction. Addition and subtraction when they are in column form is even easier and just involves applying the arithmetic on a component by component basis.

Exercise

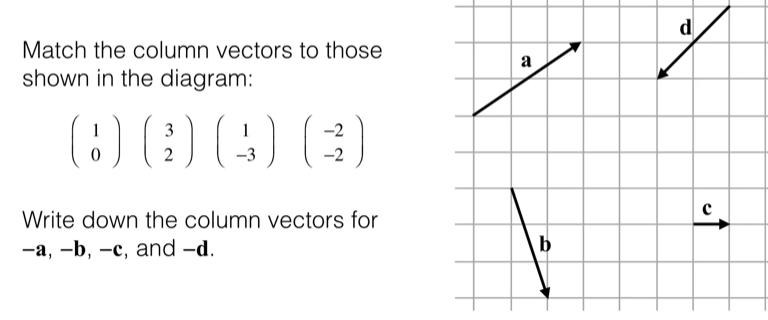
Let’s “learn by doing”, by completing exercise 19A on pages 304 and 305 of the textbook:

The answers are below:

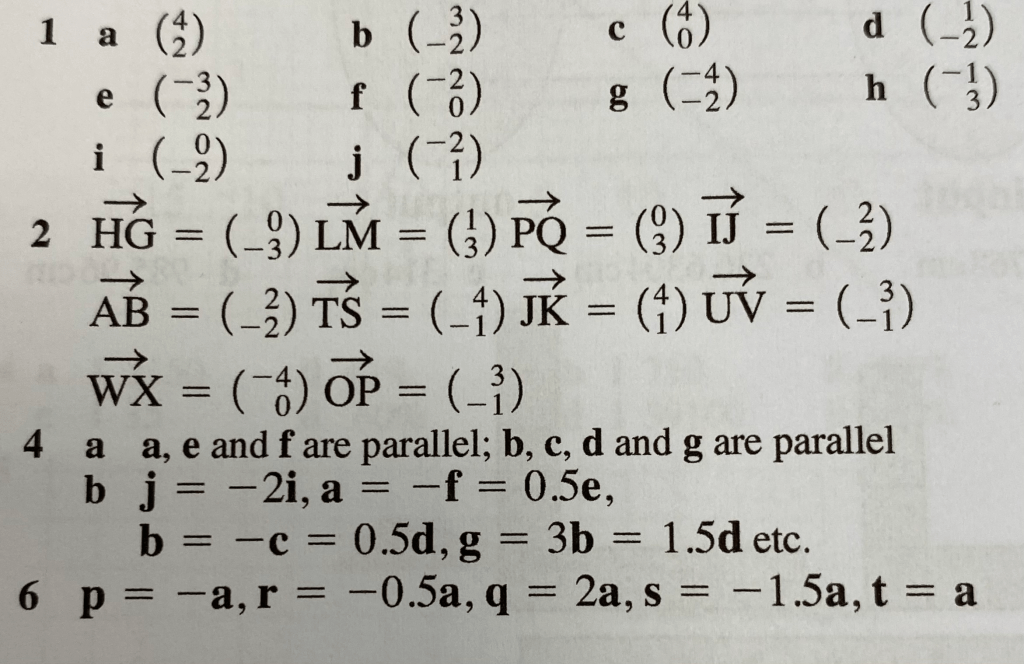
Shapes

As well as being used to describe the movement of a single point, a vector can be used to describe the movement of a whole shape, like we do when we did geometrical translations.

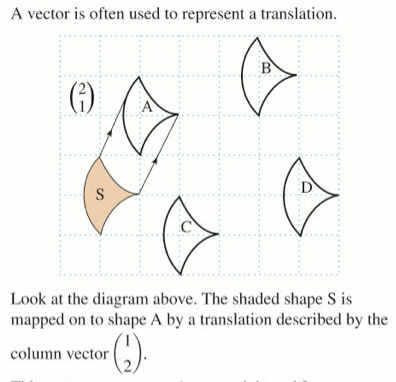
Exercise

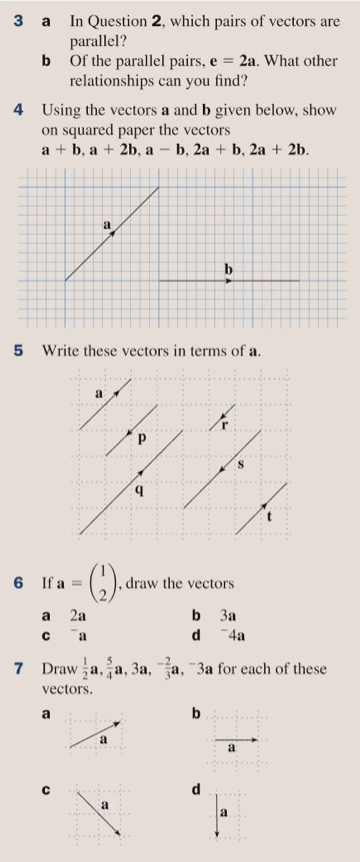
Let’s remind ourselves of how vectors are used in geometrical translations by completing exercise 19B on page 305 of the textbook:

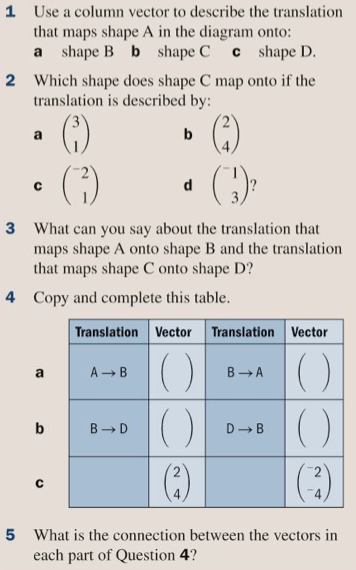
The answers are below:

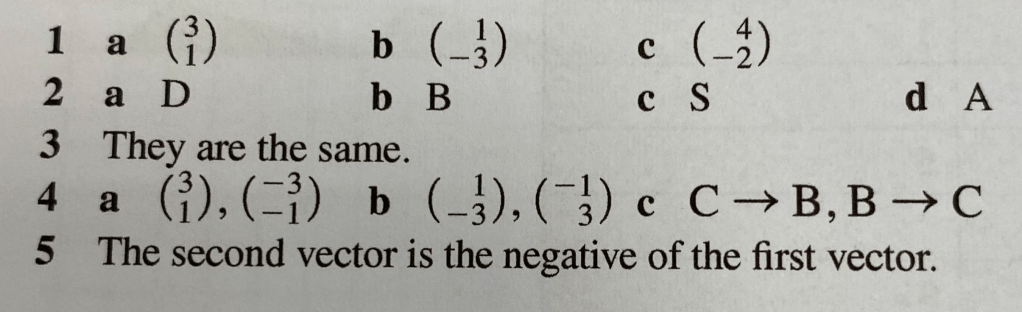
Algebraic Addition and subtraction of vectors

Vectors are easy to add and subtract in column form, we just add or subtract each of the corresponding elements. Let’s practice adding and subtracting vectors geometrically by completing exercise 19C on pages 306 and 307 of the textbook:

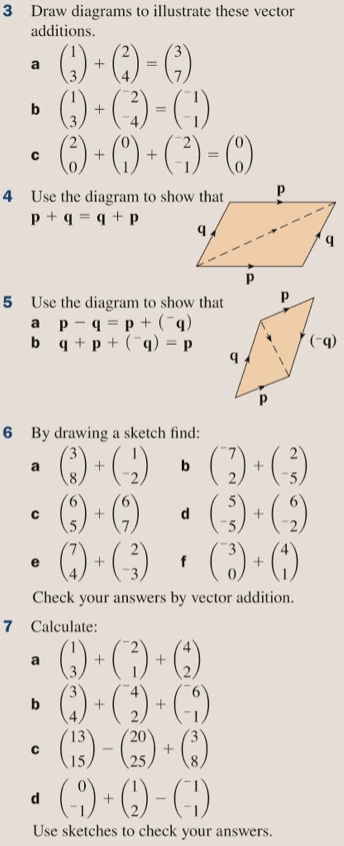
The answers are below:

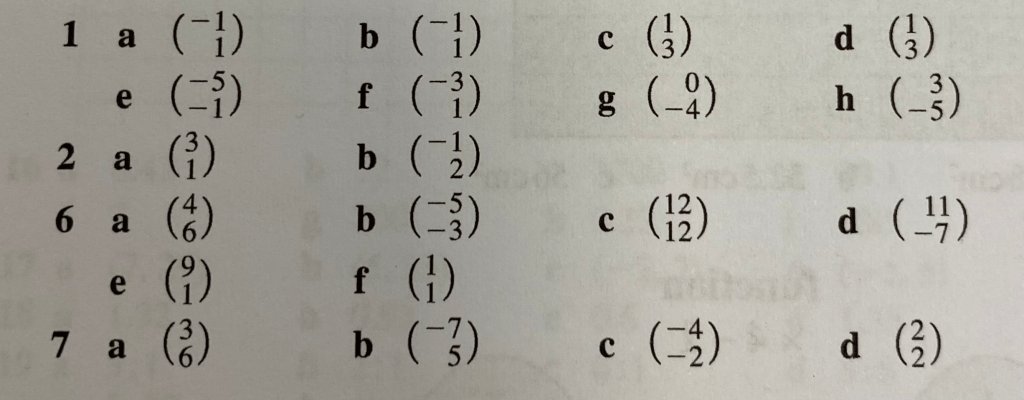
Vector arithmetic

Multiplying a vector by a scalar is straightforward, we just multiply every component of the vector by that number.

We can call the negative of a vector the inverse of the vector, as it undoes geometrically the effect of the vector.

Exercise

Let’s try some arithmetic with vectors in their algebraic form, by completing exercise 19D on pages 307 and 308 of the textbook:

The answers are below:

Another way of writing vectors is the following:

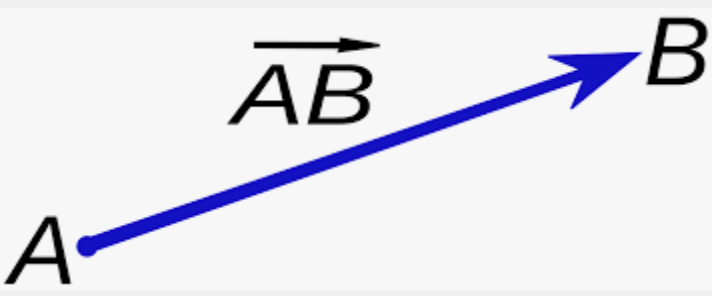
We can then tackle various geometrical problems using vector geometry.

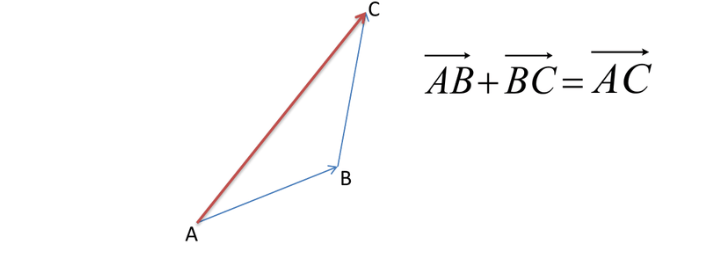
Example

Example

Exercise

Let’s complete exercise 19E on pages 308 to 309 of the textbook:

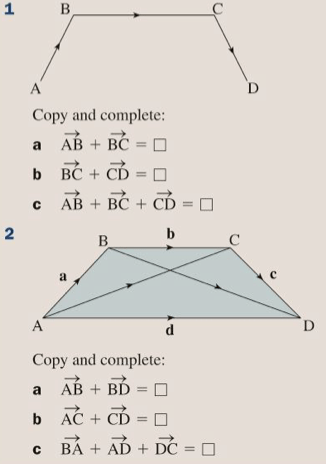
The answers are below:

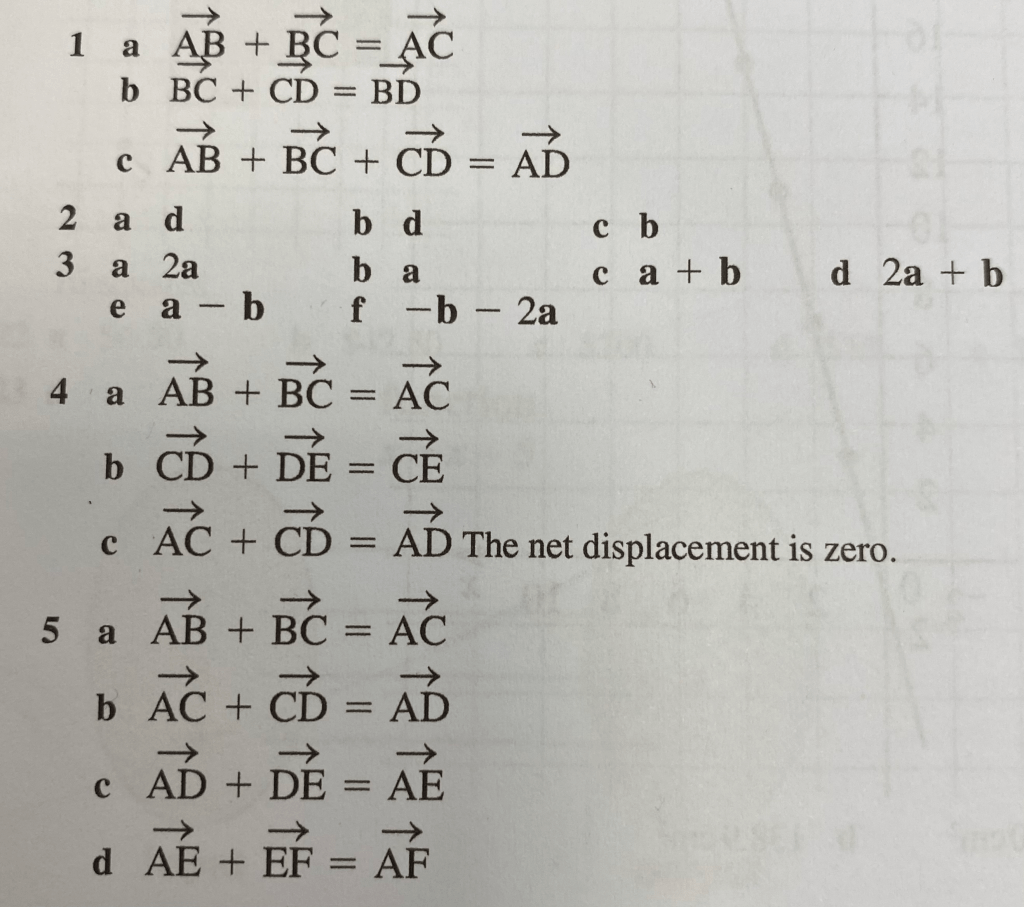
Position Vectors

As we mentioned at the start, a vector can be used to indicate a movement or translation, or it can be used to indicate a position.

This can sometimes be a little confusing, which is why it is important to clearly distinguish the two. When it used to indicate a position, the vector is always relative to the origin (or the point (0,0) in space.