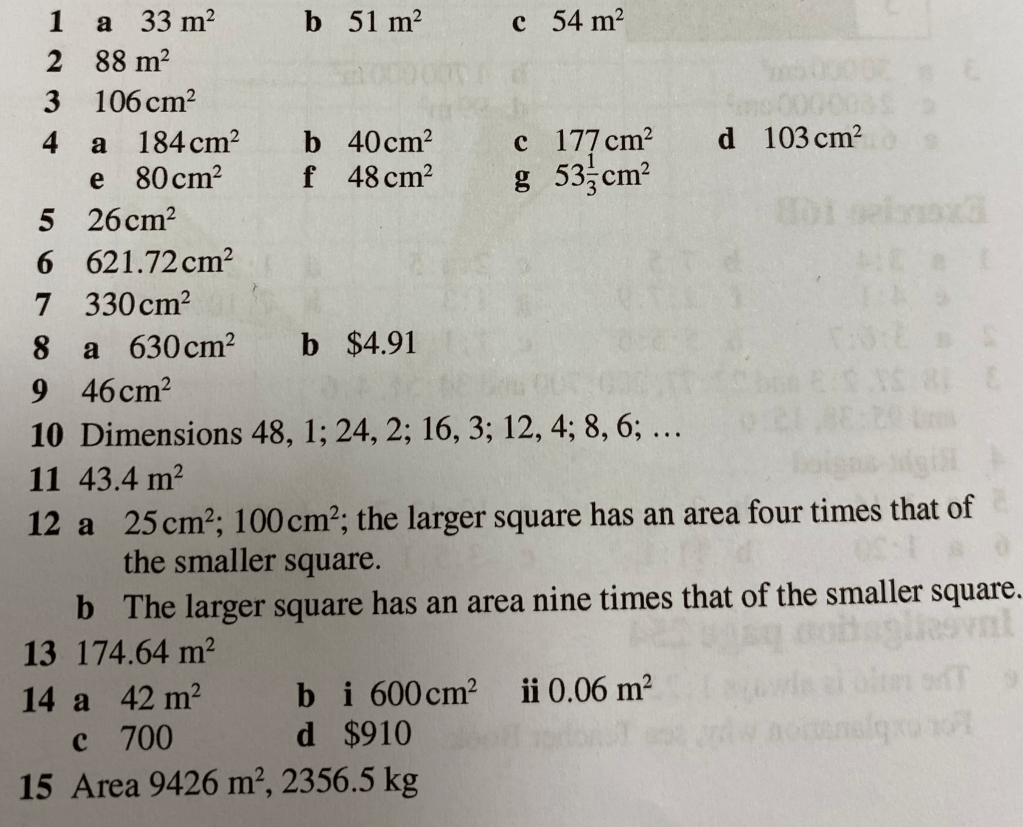After perimeter, area is the most important measure that we need to take of a shape. If you rent an apartment, it will be advertised in terms of the area of floor space that it has. Also, if you look up a country on Wikipedia, it will always tell you what area it covers (Georgia cover 69,700 square kilometres).
In our course we won’t be measuring the areas of apartments or countries, but will first master the ability to find the area of common geometrical shapes, like the triangle and the circle.
Area of a triangle
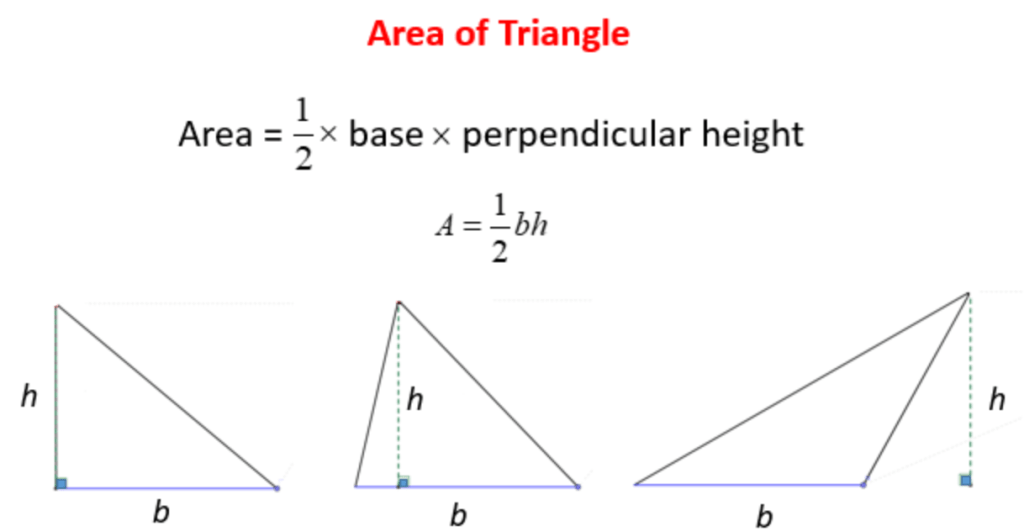
You can think of the area of a triangle as being half of the area of a rectangle with the same base length and the same perpendicular height. It doesn’t matter which side of the triangle you use as the base length, but you should always check carefully that the distance you are using as “h” really is the perpendicular height.
Example
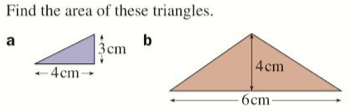
Exercise
Let’s complete exercise 17E on page 267 of the textbook:

The answers are below:

Area of a circle
Remember the special number, π which was found to be the ratio between the circumference and the diameter of all circles?
Well, I’m very happy to be able to announce that this special number also helps us to find the area of a circle.
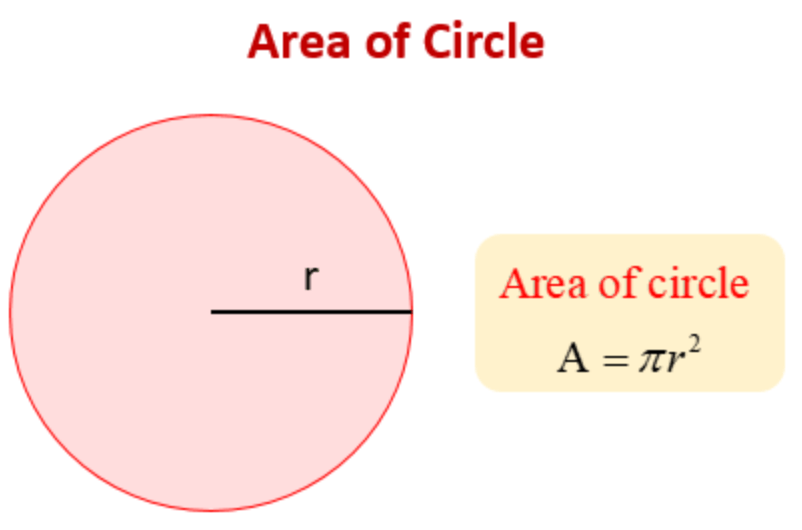
Notice that the area of a circle is given in terms of its radius. What would you do if you didn’t know the radius, but knew the diameter instead?
As we know the value of π, the formula relates “A” and “r”, so we can use it to find “A” if we know “r”, or we could also use it to find “r” if we know “A”.
Exercise
Let’s complete exercise 17G on pages 269 and 270 of the textbook:


The answers are below:

Areas of parallelograms and trapeziums
These formulae should all be written down and memorised. But let’s spend a moment or two just to remind ourselves of why they work:

Exercise
Now let’s put them into practice by completing exercises 17H and 17J:
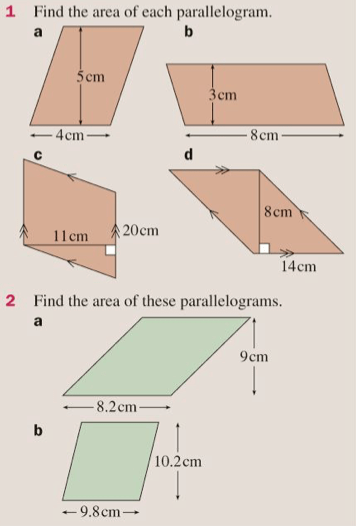
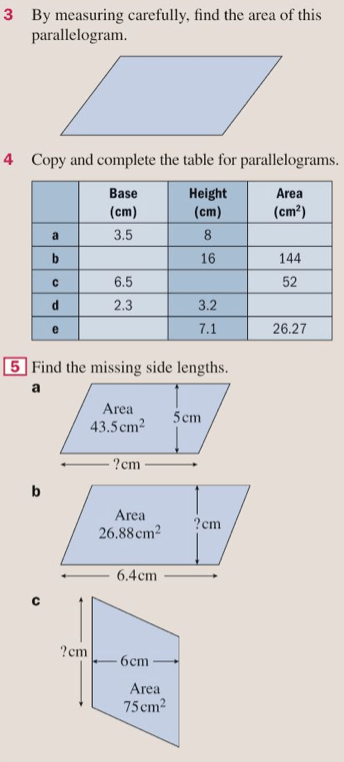
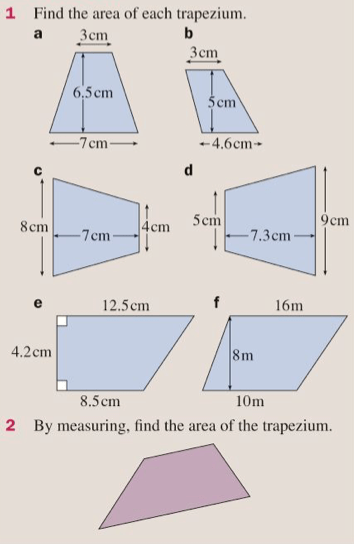

The answers are below:

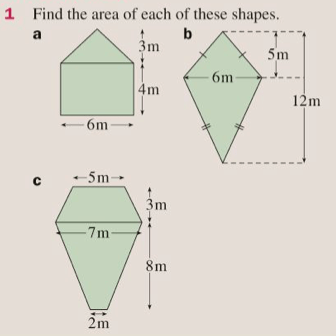
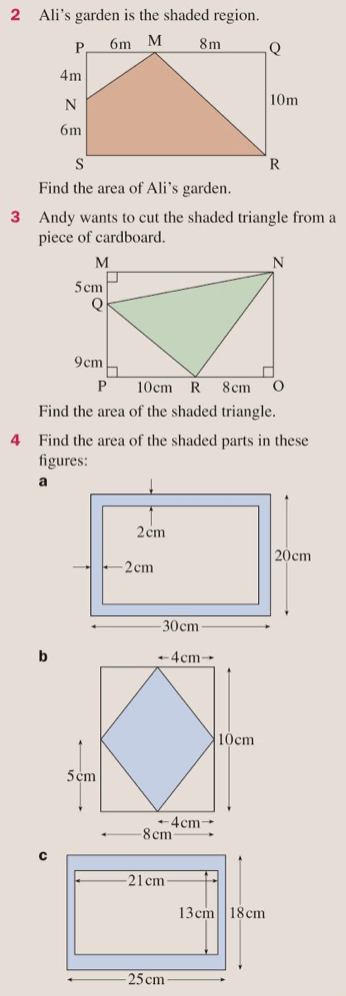
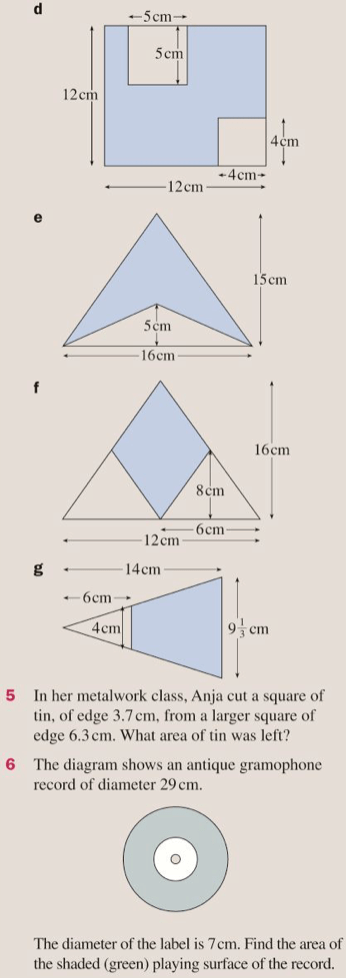
Areas of compound shapes
The good new is, that now we can find the areas of these basic shapes, we will be able to find the areas of lots more different types of shape, simply by “chopping them up” into the shapes that we already know.
Example

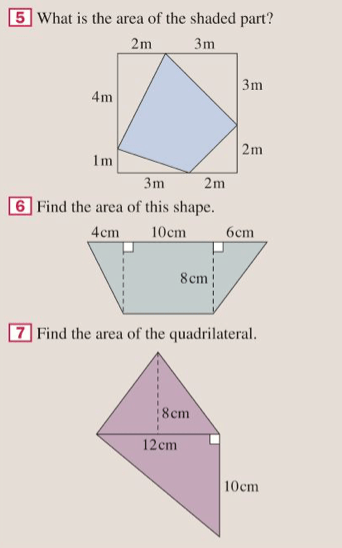
Exercise
Let’s complete exercise 17K from pages 274 to 276 of the textbook:
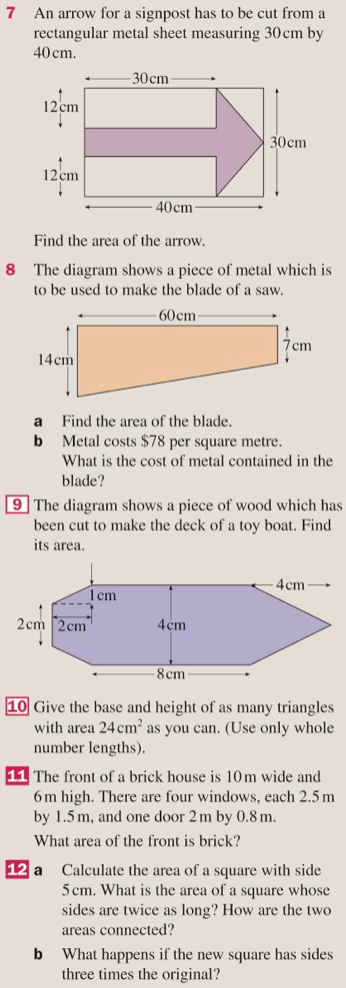

The answers are below: