In mathematics we are interested in all of the properties of shapes, as the more of them we understand, the better we are able to understand the shape.

Some of the earliest work in Geometry (which literally means “measuring the earth”) was done in Ancient Egypt, as the Nile regularly overflowed its banks and the farmers wanted to accurately measure the length of the borders of their fields (you need to know this length if you want to know what length of fencing you will need to surround it).

So one of the most important things to measure in geometry is the perimeter of a shape, which means the distance around it.

To do this we add up the lengths of each of the sides.

Example

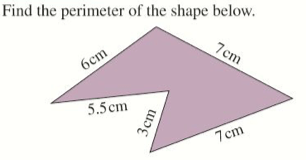
Exercise

Let’s complete the short exercise below, which is 17A from page 262 of the textbook:

The answers are below:

Circumference

In the case of a circle, its perimeter has a special name. It is called its circumference. We should know the names of some other parts of a circle too:

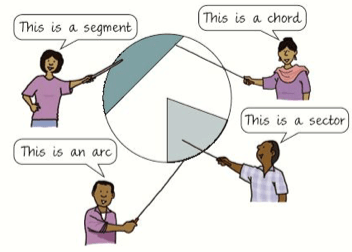
Through measurement, the Ancient Egyptians (and later the Ancient Greeks) identified that the ratio between the circumference of a circle and the diameter of a circle is always the same. They gave this number a special name, π. It is about 3.14.

Because of this, we have a formula for the relationship between the diameter, d, of a circle and the circumference, c, of a circle, which is c = πd.

Often it’s useful to think in terms of the radius of the circle, so we can adapt the formula to give c=2πr.

Example

Exercise

Let’s complete exercise 17B from pages 263 and 264 of the textbook:

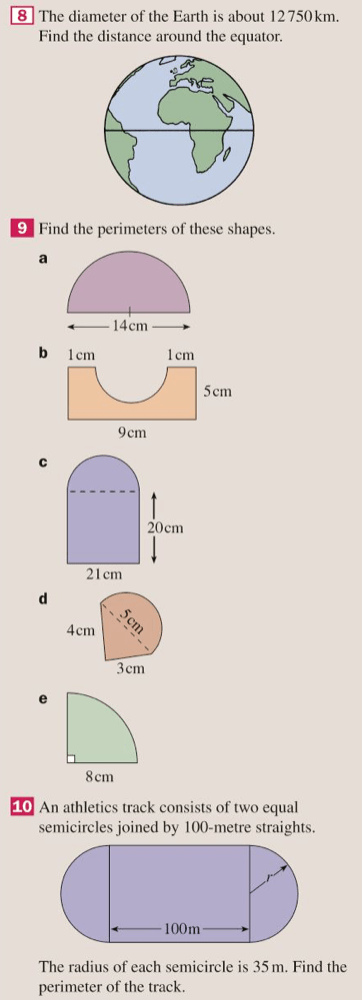
The answers are below: