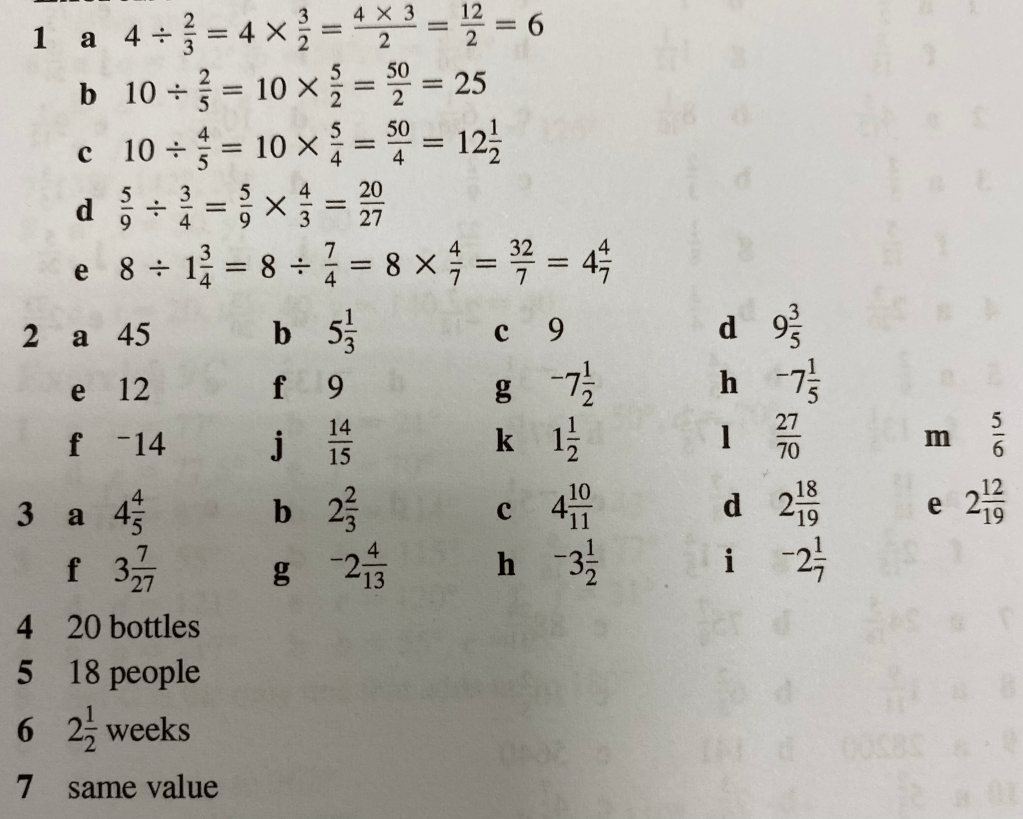The good news is that multiplying and dividing fractions is a lot easier than adding and subtracting them.

First though, let’s take a moment to think about what it means to multiply a fraction by a fraction. One association that can be helpful here is to associate the word of with multiplication.

So 1/2 of 6 is 1/2 x 6 is 3.

So if we multiply a fraction by a fraction, we are simply taking a fraction of that fractions, so for instance 1/2 x 1/2 will be what?

In terms of the procedure, it is even easier. We just multiply the numerator of the first fraction by the numerator of the second fraction to get our new numerator and we multiply the denominator of the first fraction by the denominator of the second fraction to get our new denominator.

Let’s try some examples with the teacher:

And if we are simply multiplying a fraction by an integer (remember, of course, to give your answers in simplified form):

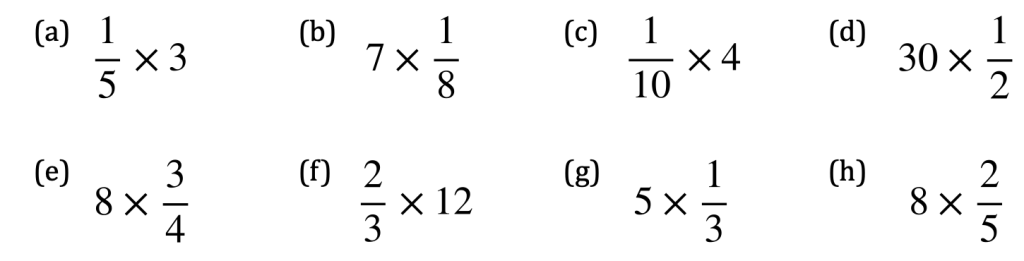
Now we can try exercise 7f on pages 106 and 107 of our textbook:

Answers:

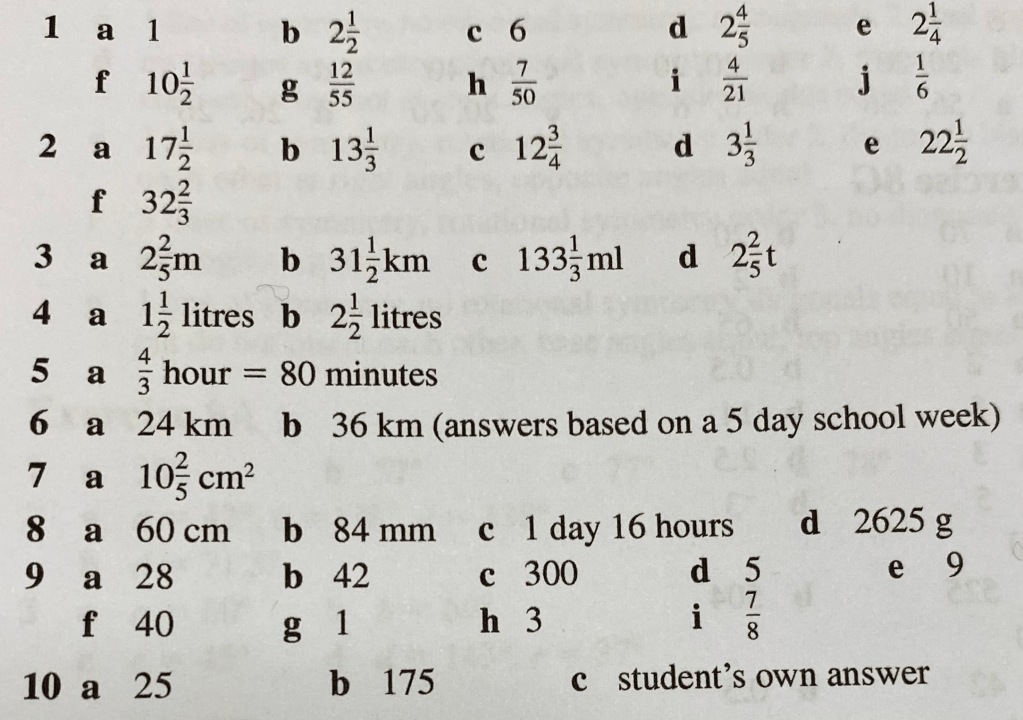
Division of fractions

As always, division is a little harder than multiplication because it is an inverse operation.

To divide by fractions we use the technique of multiplying by the fraction’s reciprocal.

The reciprocal is simply the fraction “turned upside down”.

The reason this works is because if “a” is the fraction and “b” is its reciprocal, then a x b = 1, so b = 1/a, so multiplying by b is the same as dividing by a. This is a fairly difficult idea to grasp, so don’t worry if you don’t understand it fully yet. The main thing for now is to master the technique and then you can return to this comment later to think about why it is true.

So, for instance if we want to calculate 3 ÷ 2/3, we can just calculate 3 x 3/2 = 9/2 or 4 1/2.

Let’s try some with the teacher:

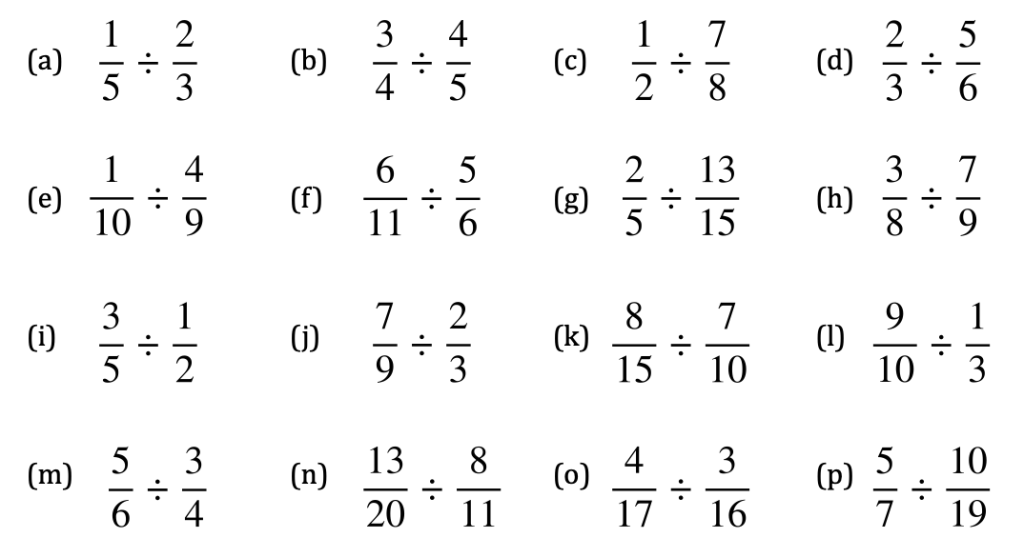
Now you can complete exercise 7H in the textbook:

The answers are below: