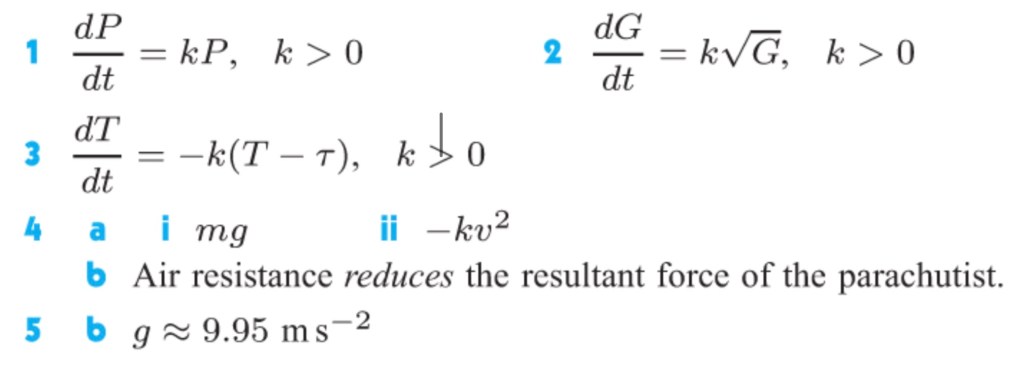Maths with David

    IBDP. AI. HL. DEs. Introduction to DEs

    Let’s start by considering a spring which is stretched by distance x, as in the image below.

    Once released from its stretched position, we can consider x as a function of t, x(t), which states the displacement of the spring from its natural equilibrium position at time, t, after being released.

    Consider the following:

    • What will happen the moment the spring is released?
    • Hooke’s Law states that the force, F, exerted by a spring, is proportional to the distance it has been stretched. Can you explain why Hooke’s Law gives us: F = -kx ?
    • Newton’s Second Law states that the acceleration of an object is proportional to the force acting on it, g iving us F = ma
    • Based on these two laws, can you see why m \frac{d^2x}{dt^2} = -kx ?
    • The solution to m \frac{d^2x}{dt^2} = -kx can be written as a cosine function. Can you see why, by considering the context, and separately by considering the equation?

    The above scenario describes a Differential Equation (“DE”) that governs the 1D motion of an extended string (the same DE governs the motion of a swinging pendulum).

    Definition: A Differential Equation is an equation whose terms include derivatives of a function

    Here are some examples of Differential Equations used outside of Pure Mathematics:

    Screenshot
    Screenshot

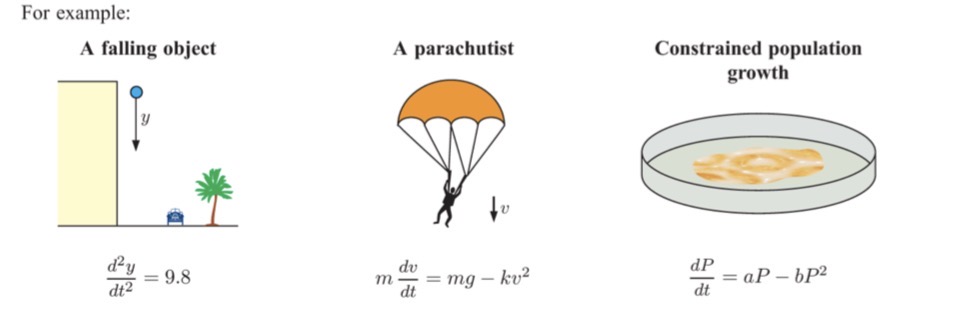
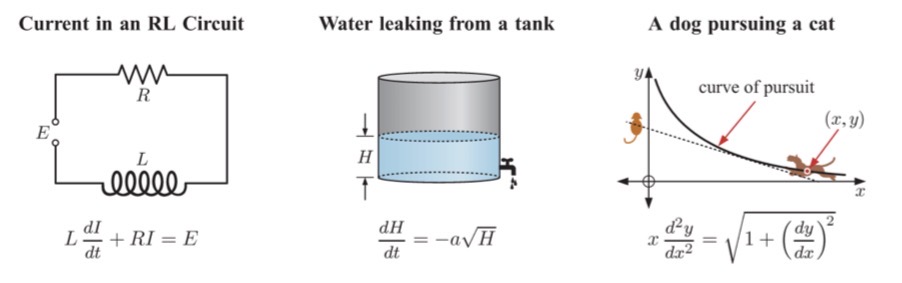
    Exercise. Constructing DEs

    1. Given sufficient resources, bacteria reproduce by “splitting” themselves at a constant rate. This means that the population P increases at a rate which is proportional to P. Write this as a differential equation.
    2. Algae is a kind of plant that grows in water. If G(t) is the amount of algae present in a pond at time t, the rate of algae growth is proportional to \sqrt{G} . Write this as a differential equation.
    3. When a hot cup of coffee cools in a room with temperature 7º, the rate at which its temperature T changes is proportional to the temperature difference with the surrounding room. Write this as a differential equation.
    4. The equation of motion for a parachutist falling with downwards velocity v, is m \frac{dv}{dt} = mg - kv^2 , k>0. The term m \frac{dv}{dt} is the resultant force, as predicted by Newton’s Second.
      • Identify the term which models:
        • Acceleration due to gravity
        • Air resistance.
      • Explain the term which has a negative coefficient
    5. Newton’s law of universal gravitation states that the force of attraction between two objects with masses m1 and m2 a distance r apart is given by F = \frac{Gm_1m_2}{r^2} where G \approx 6.7743 \times 10^{-11}m^3 kg^{-1} s^{-2}
      • Consider a small satellite with mass ms which is at altitude x above the Earth’s surface. The Earth has mass m_E \approx 5.9722 \times 10^24 kg and radius r_E \approx 6.378 \times 10^6 m .
        • Use the law of universal gravitation and Newton’s second law to show that the acceleration of the satellite due to gravity is \ddot{x} = - \frac{ Gm_E }{ (x+r_E)^2}
        • Hence estimate g, the acceleration due to gravity for an object at low altitude.

    Answers

    Screenshot