9709. S2. Linear Combinations of Random Variables

In some situations we are not interested in calculating probabilities and mean and variance for a specific random variable, but instead for a specific combination of random variables.

An example might be an investment portfolio, where each of the investments’ values could be modelled as random variables.

Expectation & Variance

Johnny has a fair six sided die with faces labelled 1, 1, 2, 2, 2, 4.

If X is the random variable “Score obtained when the dice is rolled”, then X is distributed as follows:

x	1	2	4
P( X = x )	1/3	1/2	1/6

E(X) = (1 x 1/3) + (2 x 1/2) + (4 x 1/6) = 1/3 + 1 + 2/3 = 2

Var(X) = ( (1²x 1/3) + ( 2² x 1/2 ) + (4² x 1/6 ) ) – 2² = 1

Johnny’s friend Jenny has a fair six sided die with faces labelled 4, 4, 5, 5, 5, 7.

If X is the random variable “Score obtained when the dice is rolled”, then Y is distributed as follows:

y	4	5	7
P( X = x )	1/3	1/2	1/6

E(Y) = (4 x 1/3) + (5 x 1/2) + (7 x 1/6) = 5

Var(y) = (4² x 1/3) + (5² x 1/2) + (7² x 1/6) – 5² = 1

Compare the expectations and variances of the two dice; what do you notice and why?

Reminder

For a random variable X and constant b, E(X+b) = E(X) + b and Var(X+b) = Var(X).

Also, E(aX) = aE(X) and Var(aX) = a²Var(X)

We can combine these to say that E(aX+b) = aE(X) + b and Var(aX + b) = a²Var(x)

Worked Example 1

Given that a random variable X has the probability distribution showing in the following table, find:

E(2X + 3)
Var(2X + 3)

Worked Example 2

The random variable X is the number of tails obtained when three fair coins are tossed.

Construct the probability distribution table for X and find E(X) and Var(X)
Find
- E(2X + 1)
- Var(2X + 1)

Worked Example 3

Given that the random variable X ~ B(8,0.3), find:

E(4X – 1)
Var(4X – 1)

Exercise 1

Answers

(a) 74, (b) 150
(a) 15, (b) 19.2

Worked Solutions

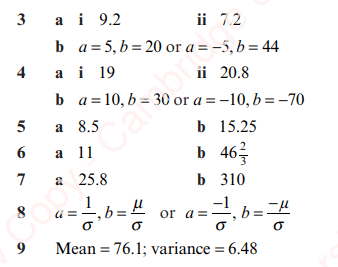
Sum and Difference of Independent Random Variables

Sasha has a green tetrahedral die with faces numbered 1, 1, 2 and 3, and a blue tetrahedral die with faces number 1, 1, 2 and 2.

What will be the mean and variance of the sums of the two dice. How do these relate to the individual means and variances of each die’s score?

If G is the score on the green die, then E(G) = 1.75 and Var(G) = 11/16

If B is the score on the blue die, then E(B) = 1.5 and Var(B) = 1/4

The table below shows the possible sums from the two dice:

+	G1	G1	G2	G3
B1	2	2	3	4
B1	2	2	3	4
B2	3	3	4	5
B2	3	3	4	5

From this we can form the random variable S, for the sum on the two dice, distributed as follows:

s	2	3	4	5
P(S=s)	1/4	3/8	1/4	1/8

From this distribution, E(S) = 3.25 and Var(S) = 15/16

Comparing with the expectation and the variance calculated for the individual dice, we note that E(G) + E(B) = E(S) and Var(G) + Var(B) = Var(S).

In general, for two independent random variables X and Y:

E(X+Y) = E(X) + E(Y) and Var(X+Y) = Var(X) + Var(Y).

Now we want to consider multiples of independent random variables, so we will make a new table, in which the numbers on the green die are doubled and the numbers on the blue die are tripled. We will again add the scores:

+	G2	G2	G4	G6
B3	5	5	7	9
B3	5	5	7	9
B6	8	8	10	12
B6	8	8	10	12

From this table we can summarise the distribution of the random variable D, such that D = 2G + 3B:

d	5	7	8	9	10	12
P(D=d)	1/4	1/8	1/4	1/8	1/8	1/8

From this distribution, E(D) = 8 and Var(D) = 5

We might note that E(D) = E(2G+3B) = 2E(G) + 3E(B) and

Var (D) = Var(2G+3B) = 2²Var(G) + 3²Var(B).

Summary

For two independent random variables X and Y and constants a and b:
E(aX + bY) = aE(x) + bE(Y) and Var(aX + bY) = a²Var(X) + b²Var(Y)

These results can be extended to any number of independent random variables.

Worked Example 4

The following tables show the probability distributions for two independent random variables, X and Y:

x	2	3	5
P(X=x)	0.2	0.3	0.5

y	0	1
P(Y=y)	0.6	0.4

Draw a probability distribution table for the random variable S, where S = X + Y, and find E(S) and Var(S).
Draw a probability distribution table for the random variable T, where T = X – Y, and find E(T) and Var(T).
E(X) = 3.8, Var(X) = 1.56, E(Y) = 0.4, Var(Y) = 0.24. Comment on your results for expectation and variance of the sum and difference of two independent random variables.

Worked Example 5

The random variable X ~ B(12,0.2) and the random variable Y~B(2,0.8).

The random variable W = X – Y. Work out the expectation and variance of W.

Discussion

What is the difference between 2X and X + X, and why are their expectations and variances not necessarily the same?

Exercise 2

Exercise 2 Answers

Exercise 2 Worked Solutions

Working with Normal Distributions

If a continuous random variable X has a normal distribution, then aX+b has a normal distribution (where a and b are constants).

If continuous random variables X and Y have independent normal distributions, then aX + bY has a normal distribution (where a and b are constants).

Worked Example 6

The masses, in kilograms, of small bags of rice and large bags of rice are denoted by X and Y, respectively, where X ~ N(2.1, 0.2²) and Y ~ N(6.6, 0.4²). Find the probability that the mass of a randomly chosen large bag is greater than three times the mass of randomly chosen small bag.

Worked Example 7

The lifetime, in months, of Duracell and Soppycell batteries have the independent distributions D ~ N(2.5, 1.1²) and S ~ N(7, 2.3²) respectively.

What is the expected total lifetime and variance of four randomly chosen Duracell batteries?
Find the probability that the total lifetime of four randomly chosen Soppycell batteries is longer than 30 months?
What is the probability that the lifetime of a randomly chosen Duracell battery is at least four times that of a Thrift battery?

Worked Example 8

A melamine worktop is made by joining sheets of melamine and chipboard. The distribution of the thickness of the chipboard, C, in mm, is C ~ N(37 , 0.3²) and the distribution of the thickness of the melamine, M, in mm, is M ~ N(1,0.01²). Assuming the distributions are independent, find the mean and variance of the thickness of the worktop if the melamine sheet is added to:

a.) Just the top surface of the chipboard;

b.) Both the top and bottom surfaces of the chipboard.

Worked Example 9

A gift package contains a set of three bars of soap. The mass, in grams, of each bar of soap is given by S ~ N(50,4²) and the packaging by T ~ N(90,5²). The gift package can be posted at a cheap rate if the mass is under 250g. Assuming that S and T are independent, find the probability that a randomly chosen gift package can be posted at the cheap rate.

Exercise 3

Exercise 3 – Answers

Exercise 3 – Worked Solutions

Linear Combinations of Poisson Distributions

If X and Y have independent Poisson distributions, then X + Y has a Poisson distribution.

If X ~ $Po( \lambda)$ and Y ~ $Po( \lambda)$ , then X+Y ~ $Po( \lambda + \mu)$ .

This result can be extended to any number of independent Poisson distributions.

Worked Example 10

Two brothers, Pasha and Sasha, keep in touch with their parents by text. The numbers of text messages sent by Pasha and Sasha are independent.

The number of text messages sent each week by Pasha has a Poisson distribution with mean 3.2.

The number of text messages sent each week by Sasha has a Poisson distribution with mean 2.5.

Write down the distribution for T, where T is a random variable defined as “the number of text messages sent each week by Pasha and Sasha”.
Calculate P(T>5).

Worked Example 11

The independent random variables X and Y are given by X ~ Po(2.4) and Y ~ Po(3.6). The random variable T = 2X – Y. Work out the expectation and variance of T. Explain why the random variable T does not follow a Poisson distribution.

Exercise 4