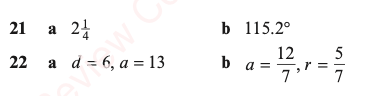9709. Pure 1. Series

Binomial Expansion

(a+b)ⁿ is called a binomial because it has two terms.

Consider the expansions (a+b)¹, (a+b)², (a+b)³, (a+b)⁴ (yes, let’s fully expand them and inspect the result). If you look at the coefficients of these do you notice any pattern?

Worked Examples

Use Pascal’s triangle to find the expansions of:
- (x+2y)³ and
- (2x-5)⁴
The coefficient of x² in the expansion of (2-cx)³ is 294. Find the possible value(s) of the constant c.

Exercise 1

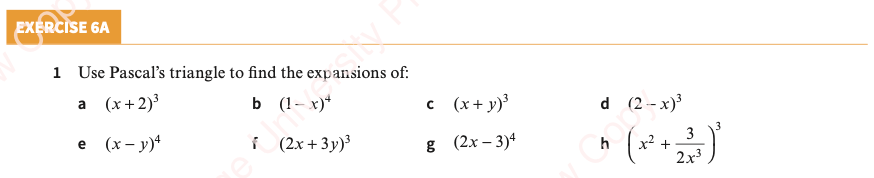
Answers

Exercise 1 Worked Solutions

Binomial coefficients

The numbers in Pascal’s triangle are actually the binomial coefficients $\binom nk=^nC_k=\frac{n!}{k!(n-k)!}$ , where n is the row of Pascal’s triangle and k goes from 1 to n from left to right in the triangle.

We can calculate these manually, or using the calculator’s buttons ‘ $^nC_k$ ‘ or ‘!’

In general, for all natural numbers n:

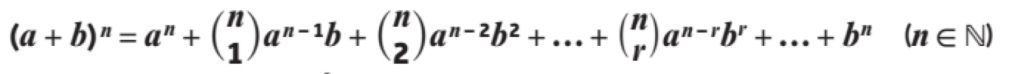
It is worth noticing that for all n, $\binom n0= 1$ , $\binom n1= n$ , $\binom nn= 1$ and for all n and k:

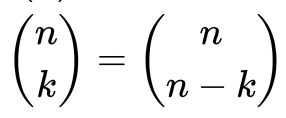
Worked Examples

Exercise 2

Answers

Exercise 2 Worked Solutions

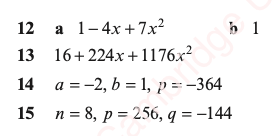
Arithmetic progression

We use the following notation:
- a or a₁ refers to the first term;
- d refers to the common difference;
- l referes to the last term.

Note that the common difference may be zero or a negative number.

The nth term is a + (n-1)d.

We use a method developed by Gauss to derive the formula for the sum of the first n terms in an arithmetic sequence. (Let’s do it!)

We should also be aware that the nth term in an arithmetic sequence is S_n-S_n-1

Worked Examples

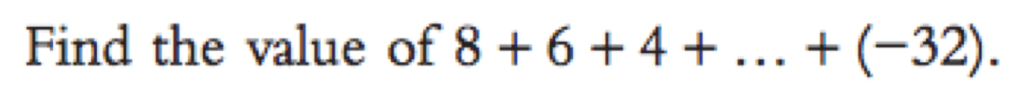
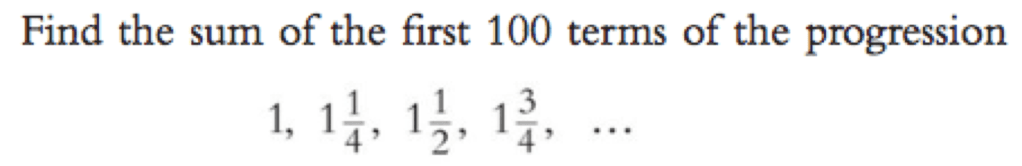
Exercise 3

Answers

Exercise 3 Worked Solutions

Geometric Progression

We use the following notation:
- a or a₁ refers to the first term;
- r refers to the common ratio;

The nth term is ar^n-1

We can multiply the whole sum by r and then subtract this to find the formula for the sum of n terms (Let’s do this!)

Worked Examples

1.) Find the seventh term in the geometric sequence: 8, 24, 72, 216, …

2.) How many terms are in the geometric sequence 4, 12, 36, …, 708588?

3.) Find the sum of 0.2 + 1 + 5 + … + 390625

Exercise 4

Answers

Exercise 4 Worked Solutions

Infinite Geometric Progressions

If the absolute value of the common ratio is less than 1, then an infinite geometric series will converge.

S_∞ = $\frac{a}{1-r}$

Worked Examples

Find the sum of the terms of the infinite progression 0.2, 0.02, 0.002, …
The first three terms of an infinite geometric progression are 16, 12 and 9.
- Write down the common ratio.
- Find the sum of the terms of the progression.

Exercise 5