Vector vs. Scalar
Notation: , a, xi + yj + zk,
. Note: i, j and k are perpendicular unit vectors (they can also be written with hats to make this clear).
a = tb <=> a is parallel to b.
a + b = b + a
Length of a is
The unit vector = a/|a| has the same direction as a, but length 1.
Types of vector
Position vector:
Direction vector:
Provided that two vectors are not parallel, any vector in 2D space can be expressed as a combination of them. In 3D space 3 vectors are needed.
= b – a
Worked Examples
Below is a hexagonal prism:
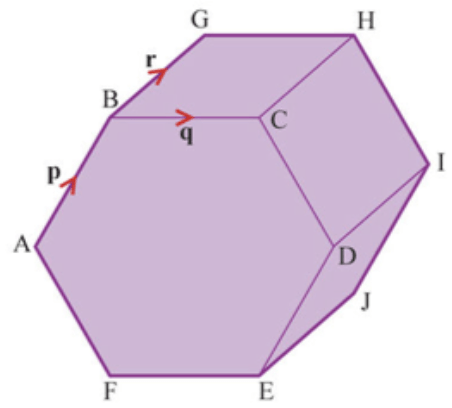
As the cross-section is regular, so .
=p,
=q and
=r. Express the following in terms of p, q and r:
Relative to an origin O, the position vectors of the points A, B and C are given by: ,
and
- Find the unit vector in the direction
;
- Find the perimeter of triangle ABC.
Exercise 1
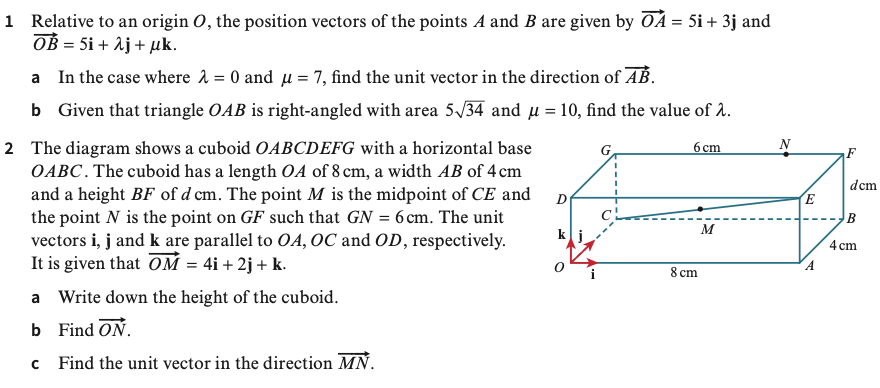


Answers


Multiplying Vectors
We can multiply vectors using a vector product / cross product, which gives us a vector (not in our syllabus), or using the scalar product / dot product that gives us a scalar.
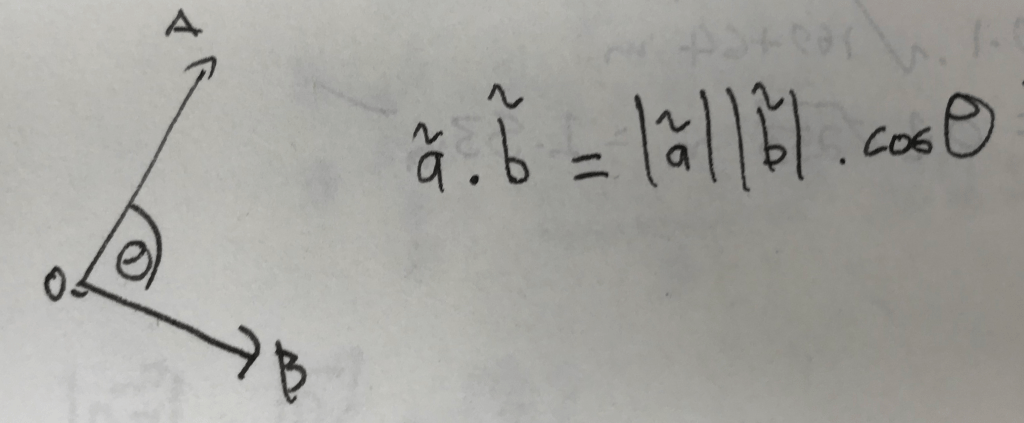
The scalar product represents the impact of one of the vectors on the others.
So if the vectors are parallel, is 1 and so the vectors magnitudes are multiplied together, but if the are perpendicular,
is zero, so there is not impact.
So, to summarise, if a is parallel to b, then a.b = |a|b| and if a is perpendicular to b then a.b = 0.
Worked Examples
1.) The points P, Q and R are (1,0,-1), (2,4,1) and (3,5,6). Find the angle QPR.
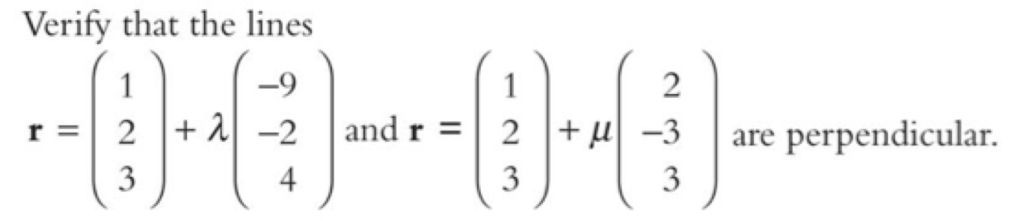
Exercise 3


Answers
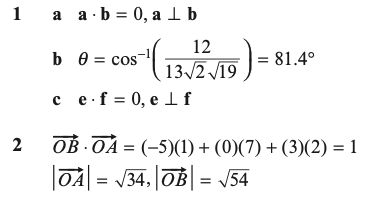


Vector Equation of a Line
To define a line, we need one vector to define the position of the line, and another to define the direction of the line, so a line r = a + tb.
If we know two points on the line, but don’t know the direction, then we can express the line as r=a+t(c–a).
To find the angle between two lines we must find the angle between the two direction vectors of the lines.
The parametric form is basically the same as the vector form, but we specify it as three separate equations: x=aX+tbX, y=aY+tbY, z=aZ+tbZ.
If we know a point P:(x1,y1,z1) and a line r = a + tb, then we can find the distance between the point and the line by taking an arbitrary point on the line N:(a1+tb1, a2+tb2, a3+tb3), and then using the fact that .b = 0, as the shortest distance to the point is perpendicular to the line to calculate t.
Worked Examples
1.) Point A has coordinates (-2,4,1) and point B has coordinates (2,1,3)
- Find the vector equation of the line AB
- Does the point (6,-2,7) lie on the line AB?
- The point N lies on the line AB. Given that 3|AN|=|NB|, find the coordinates of N.
2.)

3.)

Exercise 3

Answers


Types of Line and Intersections
2 distinct lines in 3D space must either be: parallel, skew, or intersecting.
To test if they are parallel we test if one direction vector is a multiple of the other
To test if they intersect we treat two of the dimensions as a system of two equations and solve them. If the solution also solves for the third dimension, then they intersect, and the solution is their intersection point.
Worked Examples
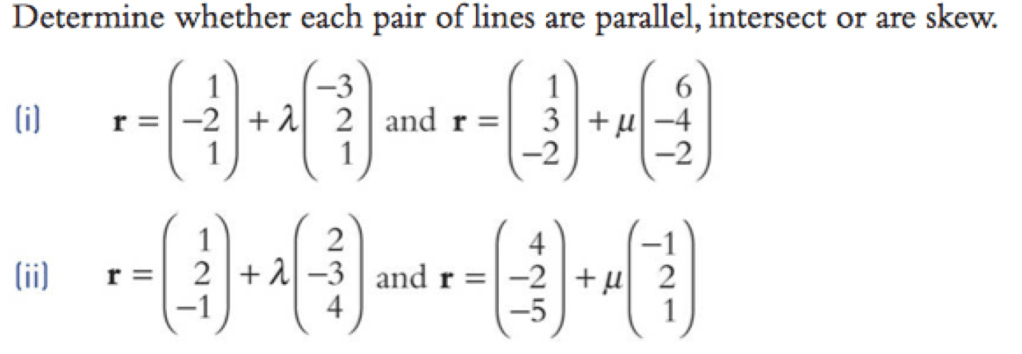
Exercise 4


Mixed Exercise


Exercise Answers

Mixed Exercise Answers


