Maths with David

    9709. P3. Numerical Solutions. Past Exam Questions

    9709/31/M/J/25q9 – Mark Scheme

    The constant s is such that \int_1^a 6x lnx dx = 4 .

    (a) Show that a = exp( \frac{1}{6}( \frac{5}{a^2 } +3 ) [5 marks]

    (b) Verify by calculation that a lies between 2 and 2.1. [2 marks]

    (c) Use an iterative formula based on the equation in part (a) to determine a correct to 2 decimal places. Give the result of each iteration to 4 decimal places. [3 marks]

    9709/32/M/J/25q6 – Mark Scheme

    (a) By sketching a suitable pair of graphs, show that the equation \vert x-2 \vert = 2 sin \frac{1}{2} x has only one root in the interval 0 < x < \pi [2 marks]

    (b) Show by calculation that this root lies between 1 and 1.5 [2 marks]

    (c) Use the iterative formula x_{n+1} = 2 - 2sin \frac{1}{2} x_n with an initial value of 1.03 to calculate the root correct to 2 decimal places. Give the result of each iteration to 4 decimal places. [3 marks]

    9709/33/M/J/25q11 – Mark Scheme

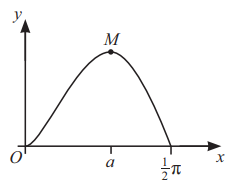
    The diagram shows the curve y = \sqrt{x} sin2x for 0 \leq x \leq \frac{1}{2} \pi . The curve has a maximum point at M, where x = a.

    (a) Show that tan 2a = -4a [4 marks]

    (b) Show by calculation that 0.9 < a < 0.95 [2 marks]

    (c) Show that if a sequence of values given by the iterative formula x_{n+1} = \frac{1}{2}( \pi - tan^{-1}(4x_n)) converges, then it converges to a. [2 marks]

    (d) Use the iterative formula in part (c) to calculate a correct to 4 decimal places. Give the result of each iteration to 6 decimal places. [3 marks]