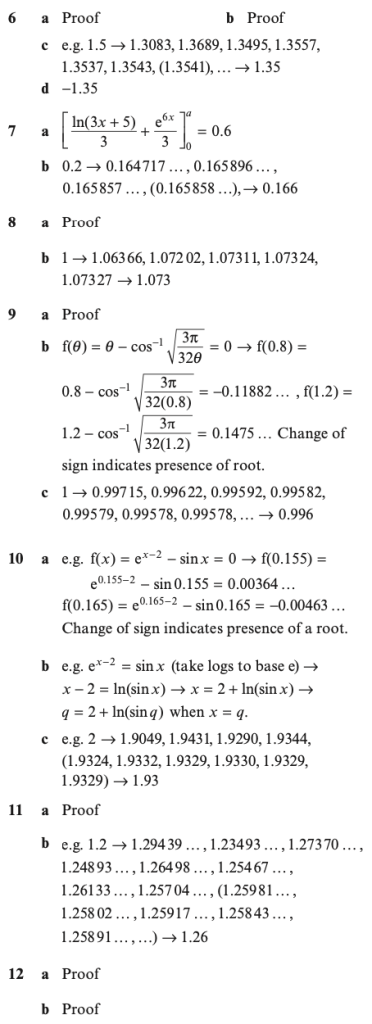What are numerical methods? Why do we need them? What can be solved by them? How accurate are they? How efficient are they?
Iteration
What does iteration mean? What is an iterative formula?
Before starting an iterative process, we need to find the approximate location of a root.
This can be done with the help of graphical methods or by trial and error. The result is the first value we use in our iterative process.
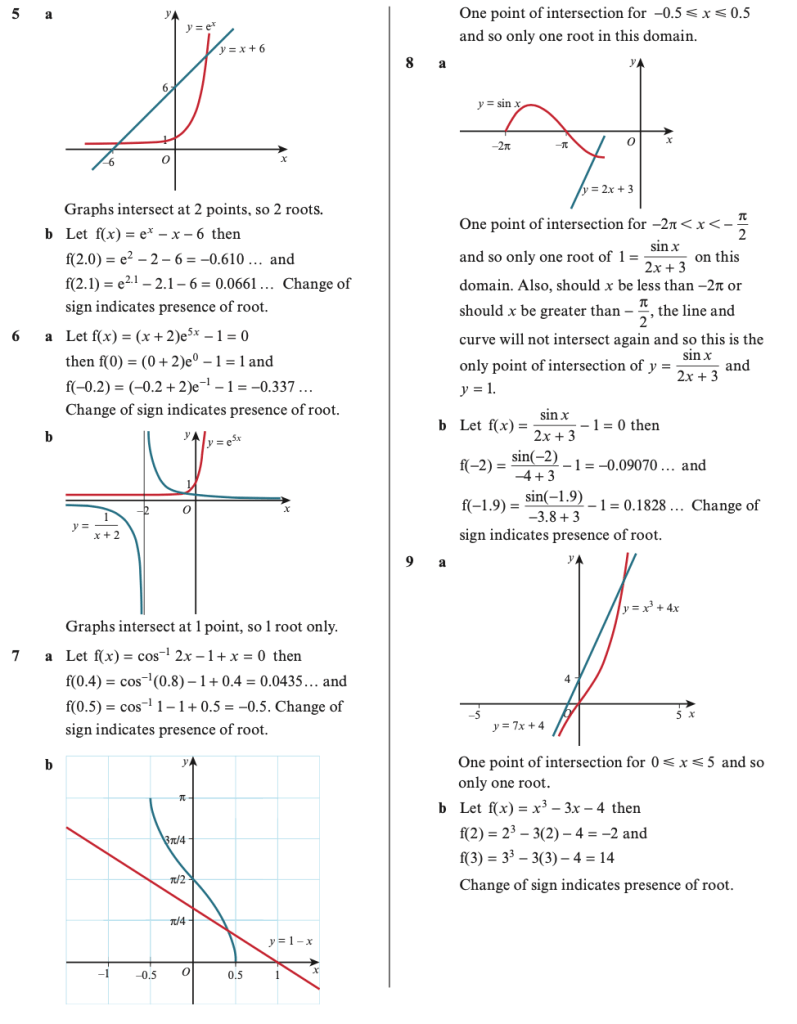
Worked Examples
1.) The diagram below shows a sketch of the curve y=f(x), where f(x) = x3-4x2+3x+1:
- Explain how the graph shows that f(x) has a root between x=2 and x=3.
- Show that f(x) has a root between x=1.4 and x=1.5.
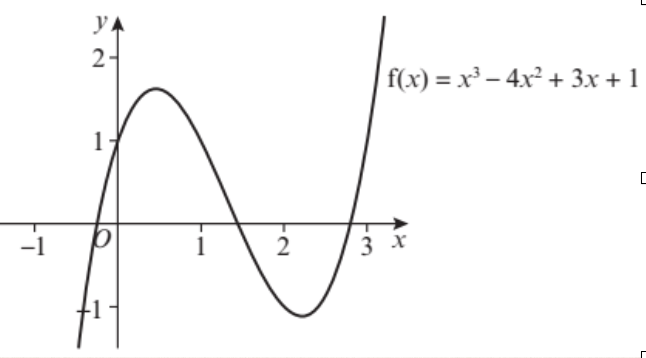
2.) The diagram below shows a graph of the function f(x) = 54x3 – 225x2 + 309x – 140. A student observes that f(1.1) and f(1.6) are both negative and states that f(x) has no roots in the interval (1.1,1.6).
- Explain with reference to the diagram why the student is incorrect.
- Calculate f(1.3) and f(1.5) and use your answer to explain why there are at least 3 roots in the interval 1.1 < x < 1.7.
Exercise 1



Answers



Then what next?
When we have found the approximate location of a root, what methods can we use to get closer to it?
Interval bisection -> Not on syllabus, but there are various numerical methods to efficiently hone in on the roots
Iterative methods -> we rearrange the equation from the form f1(x) = 0 into the form f(x) = x and form an iterative formula, which may or may not work.
Why (and when) do iterative formulae work?
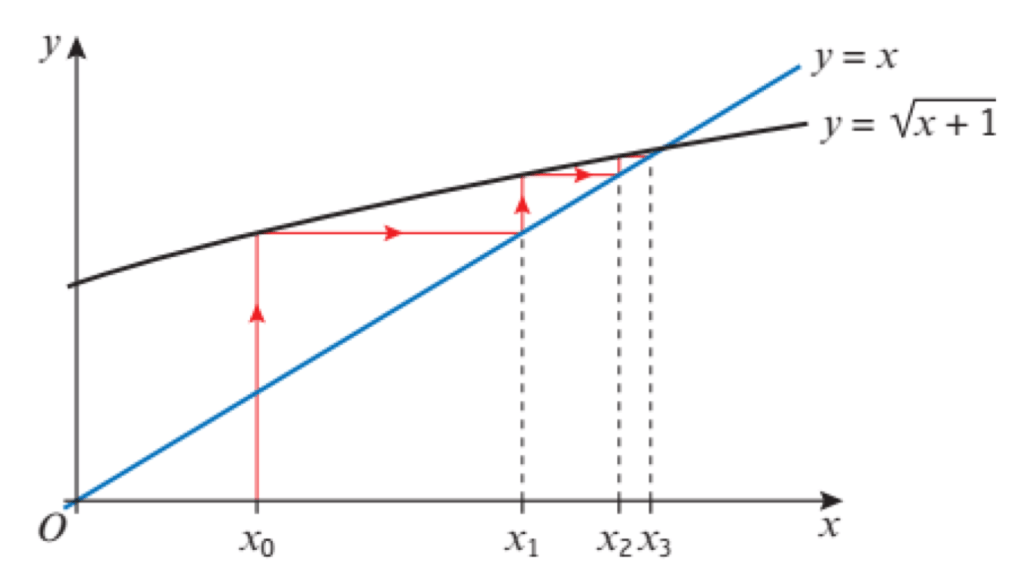

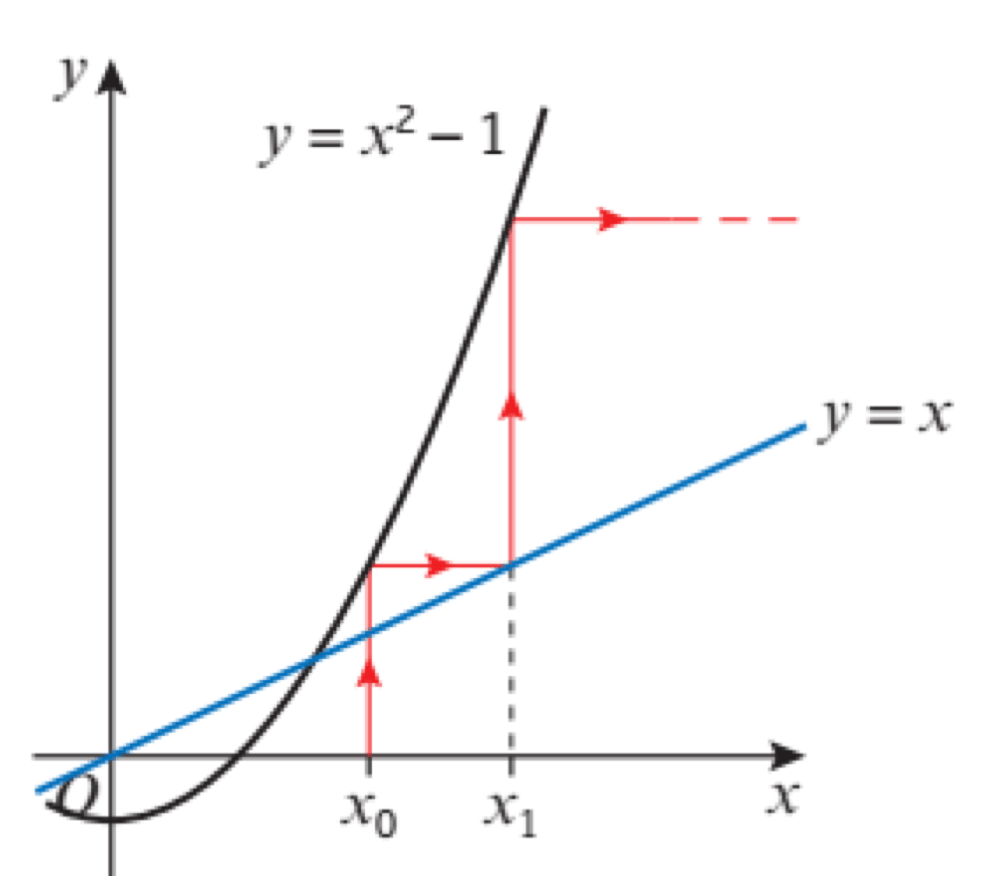
Choosing a convergent iterative formula
There are many methods for choosing an iterative formula that converges. But Cambridge will tell you which formula works. In general, the curve of the equation y = RHS needs to be concave downward.
Good use of calculators, including use of the ‘ANS’ button, the arrows and the formula bar is essential to efficiently answer numerical methods questions.
Worked Examples
1.) f(x)=x2-4x+1. Show that the equation f(x) = 0 can be written as x≠0.
f(x) has a root, 𝛼, in the interval 3 < x < 4. Use the iterative formula with x0=3 to find the value of x1, x2 and x3.
2.) f(x) = x3-3x2-2x+5. Show that the equation f(x)=0 has a root in the interval 3<x<4
Use the iterative formula to calculate the value of the root correct to 3 decimal places, showing each of your iterative answers to 4 decimal places and taking:
- x0 = 1.5
- x0 = 4
Exercise 2



Answers



Application of Numerical Methods in Other Areas of Mathematics
The diagram below shows a sketch of part of the curve with equation v=f(t), where f(t) = (10 – ½(t+1))ln(t+1):
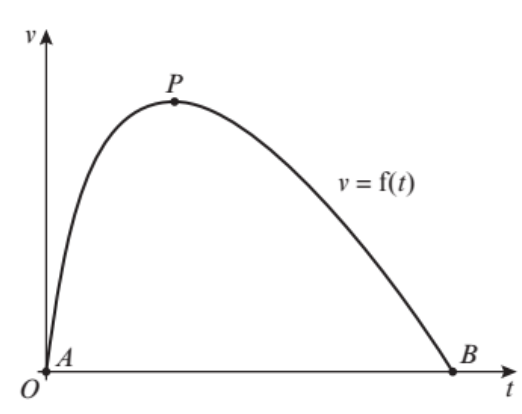
The function models the velocity in metres per second of a skier travelling in a straight line.
- Find the coordinates of A and B
- Find f'(t)
- Given that P is a stationary point on the curve, show that the t-coordinate of P lies between 5.8 and 5.9
- An approximation for the t-coordinate of P is found using the iterative formula
. Let t0=5 and find the values of t1, t2 and t3, giving your answers to 3 decimal places.
Exercise 3

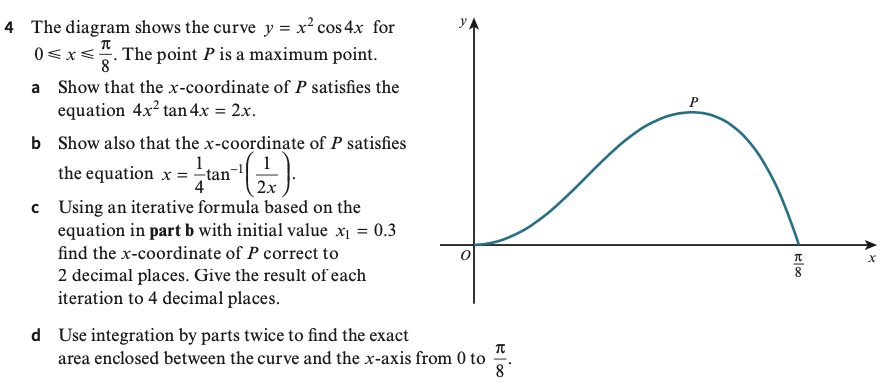
Mixed Exercise

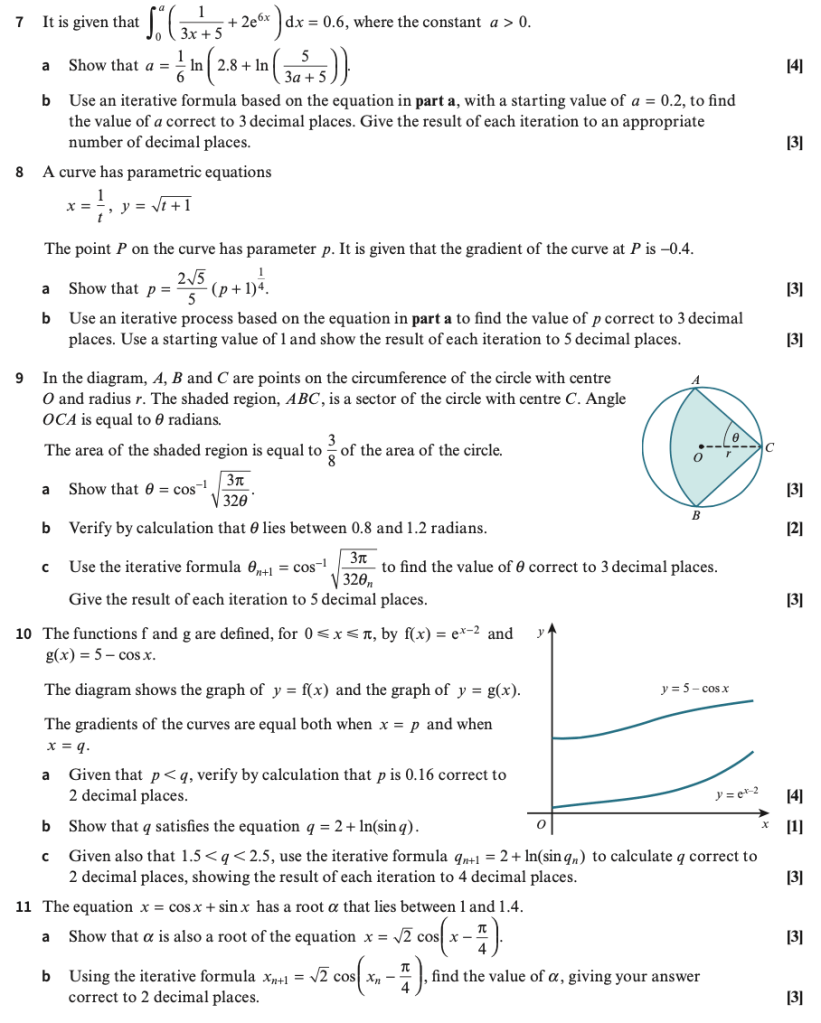
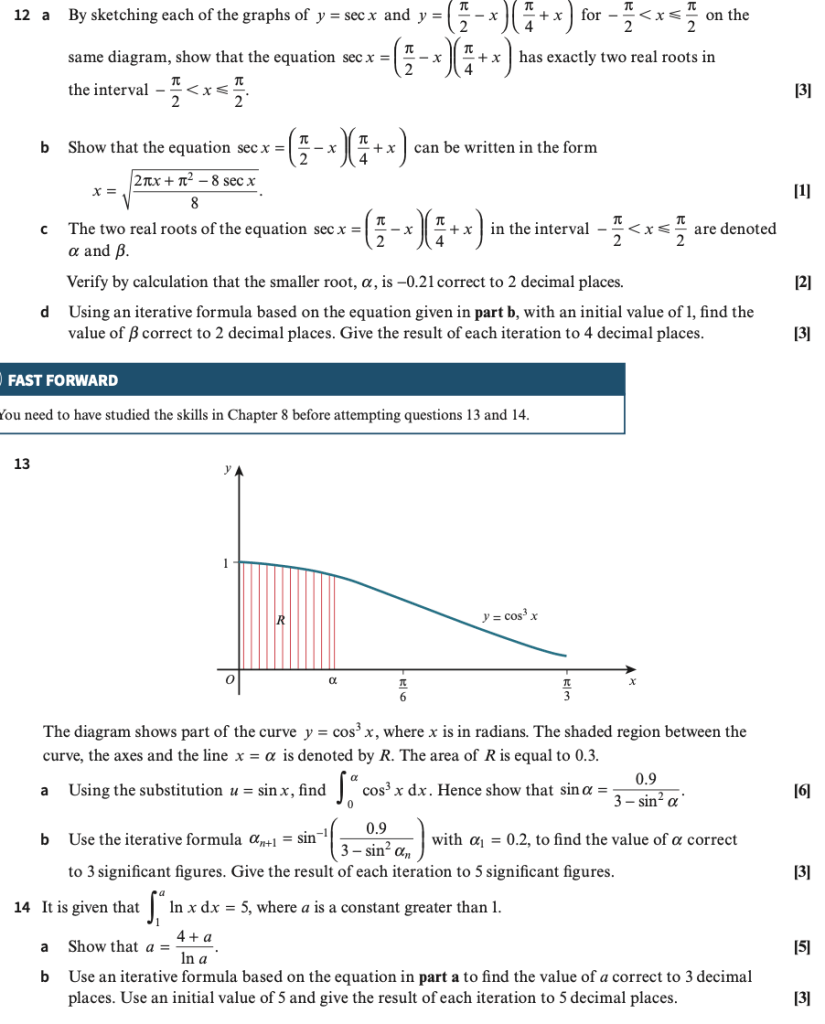
Exercise 3 Answers


Mixed Exercise Answers