Maths with David

9709. P3. Integration

Just like division is the inverse of multiplication (and typically a little more difficult), so if we want to find 72÷3 we can recognise that 3×24=72, so 72÷3 is 24. So, with integration, if we want to integrate f(x) we can think about what function we would differentiate to get f(x).

Integrating exponential functions

As we know that $\frac{d}{dx}(e^{ax+b})=ae^{ax+b}$ , so we can recognise that: $\int e^{ax+b} dx = \frac{1}{a}e^{ax+b}+c$ .

Worked Examples

1.) Find the following integrals:

$\int e^{2x-3} dx$ ;
$\int_1^5 6e^{3x} dx$ .

2.) The diagram below shows the graph of y=e^x. The point A has coordinates (ln5,0), B has coordinates (ln5,5) and C has coordinates (0,5):

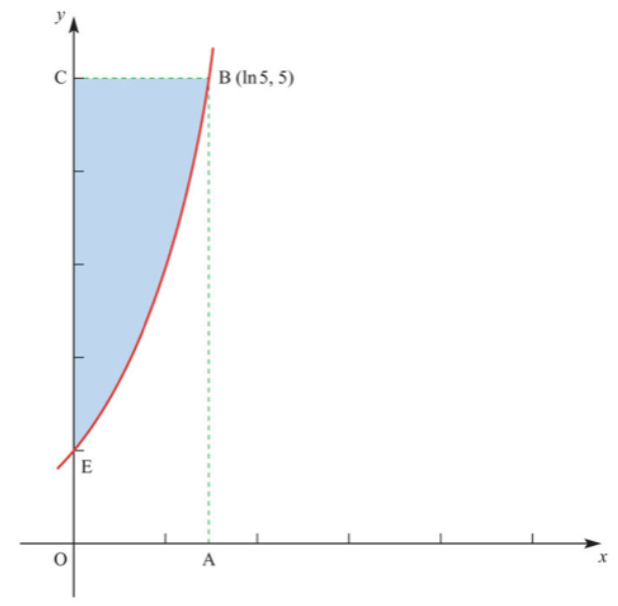
Find the area of the region OABE enclosed by the curve y=e^x, the x-axis, the y-axis and the line AB. Hence find the area of the shaded region EBC;
The graph of y=e^x is transformed into the graph of y = lnx. Describe this transformation geometrically.

3.) A curve is such that $\frac{dy}{dx} = e^{2x}-2e^{-x}$ . The point (0,1) lies on the curve.

Find the equation of the curve
The curve has one stationary point. Find the x coordinate of this point and determine whether it is a maximum or a minimum point.

Exercise 1

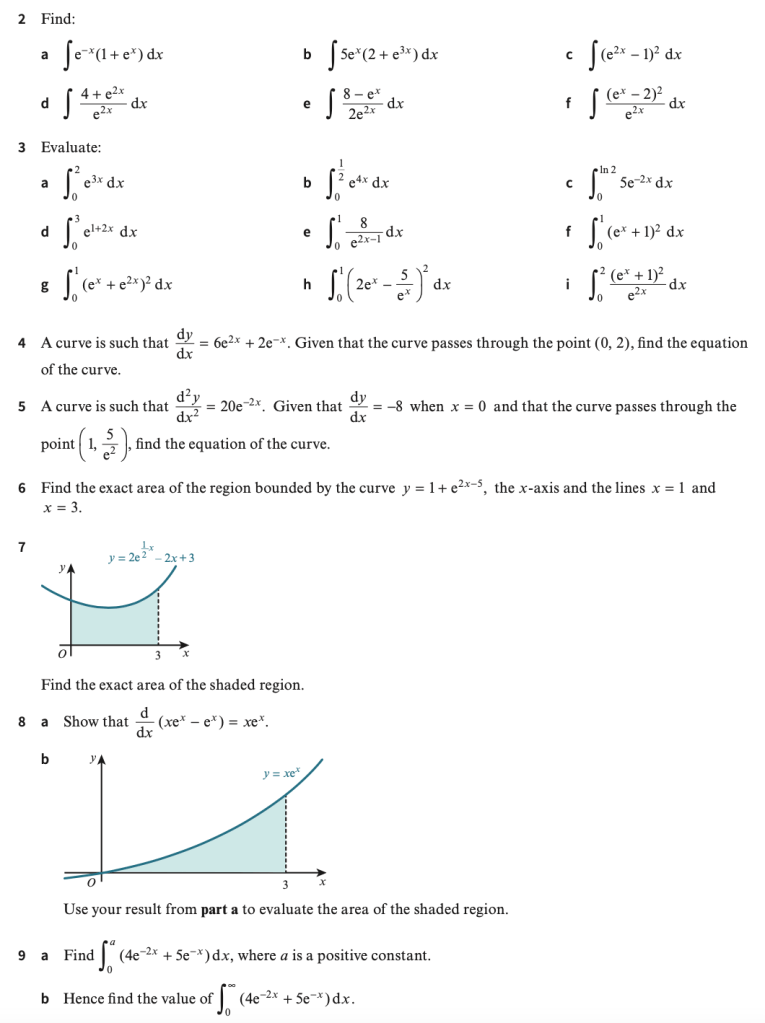
Answers

Exercise 1 Worked Solutions

Integrating Linear Reciprocal Functions

$\int \frac{1}{x} dx = ln|x|+c$

$\int \frac{1}{ax+b} dx = \frac{1}{a}ln|ax+b|+c$

N.B. Textbooks often do not write the modulus sign when doing indefinite integration. It is better to always write it.

Worked Examples

1.) Given that a is a positive constant and $\int_a^{3a} \frac{2x+1}{x}dx=ln12$ , find the exact value of a.

2.) Integrate the following functions:

$\frac{1}{3x+2}$
$\frac{1}{2x+1}$
$\frac{3}{1-4x}$ .

3.) Given $\int_{e^2}^{e^8} \frac{1}{kx}dx =\frac{1}{4}$ , find the value of k.

Exercise 2

Answers

Exercise 2 Worked Solutions

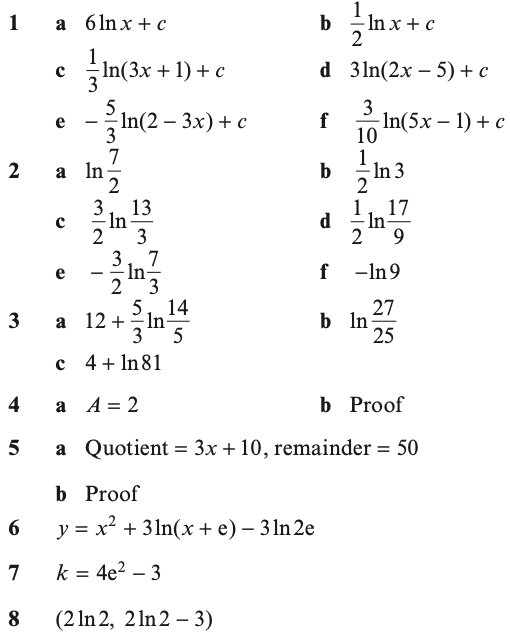
Integrating Trigonometric Functions

Theory

$\int cosx dx = sinx+c$

$\int sinx dx = -cosx+c$

$\int sec^2x dx = tanx+c$

$\int cos(ax+b) dx = \frac{1}{a}sin(ax+b)+c$

$\int sin(ax+b) dx = -\frac{1}{a}cos(ax+b)+c$

$\int sec^2(ax+b) dx = \frac{1}{a}tan(ax+b)+c$

Worked Examples

1.) Find the following integrals:

$\int (2cosx + \frac{3}{x} - \sqrt{x})dx$ ;
$\int cos(2x+3) dx$
$\int e^{4x+1} dx$
$\int sec^2 3x dx$

Exercise 3

Answers

Exercise 3 Worked Solutions

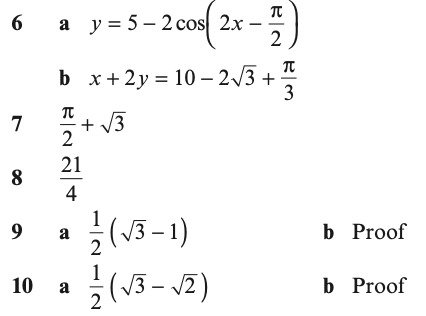
Integrating using trigonometric identities

We can use the double angle formulae to help us integrate sin²x or cos²x.

Pythagoras’ theorem is also useful.

Cos 2A = cos²A-sin²A = 2cos²A – 1 = 1-2sin²A

1+tan²x=sec²x

1+cot²x=cosec²x

Worked Examples

1.) Find $\int tan^2x dx$

2.) Show that $\int_{\pi/12}^{\pi/8}sin^2x dx = \frac{\pi}{48} + \frac{1-\sqrt{2}}{8}$

3.) Find $\int sin3xcos3x dx$

Exercise 4

Mixed Exercise

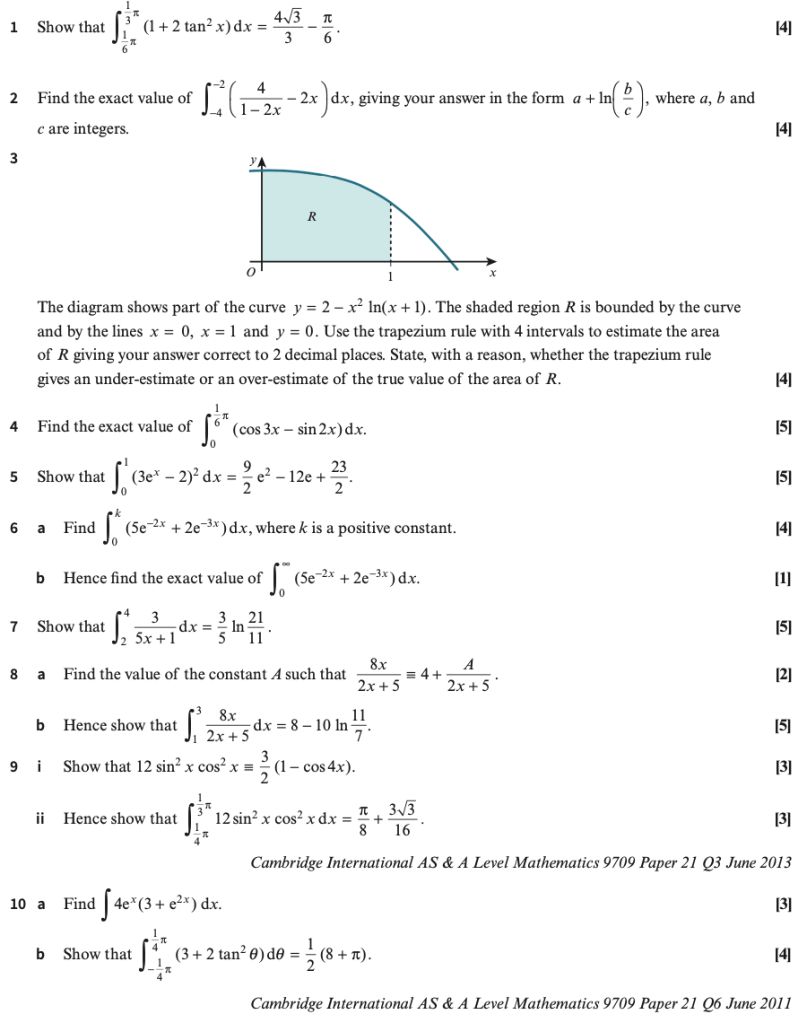
Exercise 4 Answers

Mixed Exercise Answers

Exercise 4 & Mixed Exercise Worked Solutions