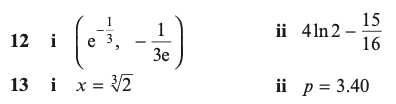Differentiating tan-1x
If y = tan-1x, then x=tany.
We can differentiate both sides of this equation with respect to x (using implicit differentiation on the RHS) and then use Pythagoras’ Theorem on the result to get:
Worked Examples
Find in terms of x for each of the following:
- y=tan-12x;
- y=tan-13x;
- y=tan-1(x/2);
- y=tan-1(x/3).
Exercise 1
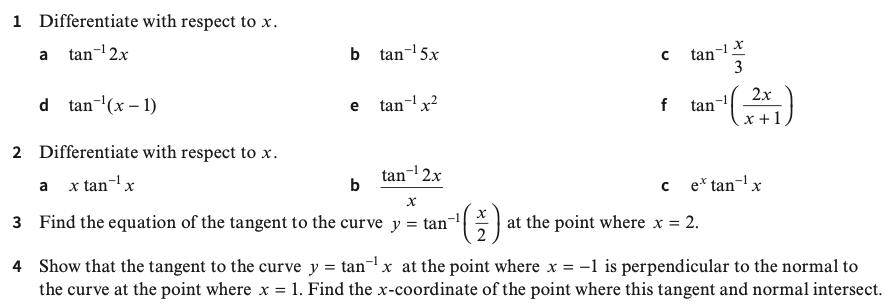
Answers

Integration of
Based on the derivative of tan-1x, we can see that:
If the x2 has a coefficient, it is convenient to start by “moving it outside” the integral sign, eg:
Worked Example
1.)
2.)
3.) Find the indefinite integral of
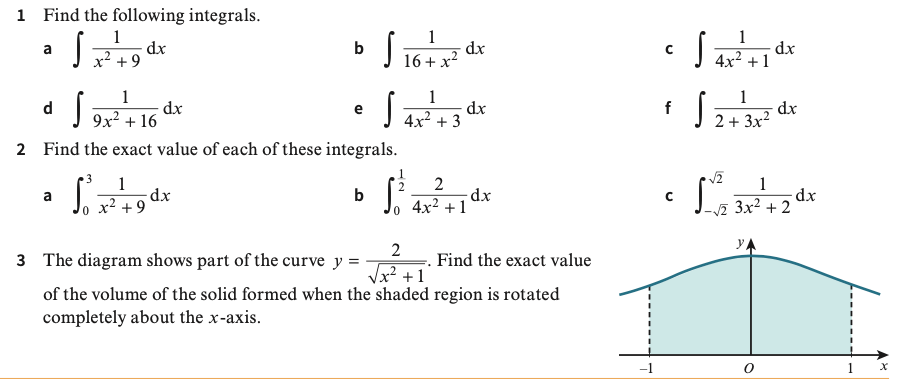
Exercise 2
Answers
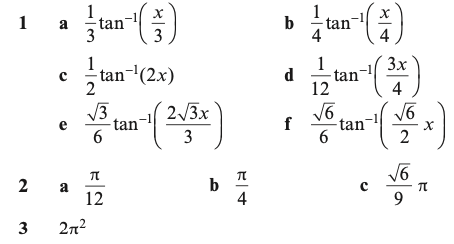
Integration of
As with other examples, we may sometimes need to modify an expression slightly to get it into this form, for example taking a constant outside of the integral sign.
Worked Examples
1.)
2.)
3.)
4.)
5.)
Exercise 3
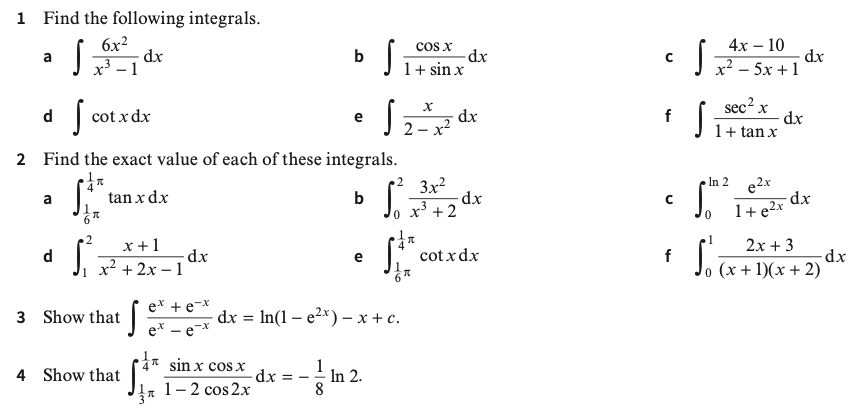
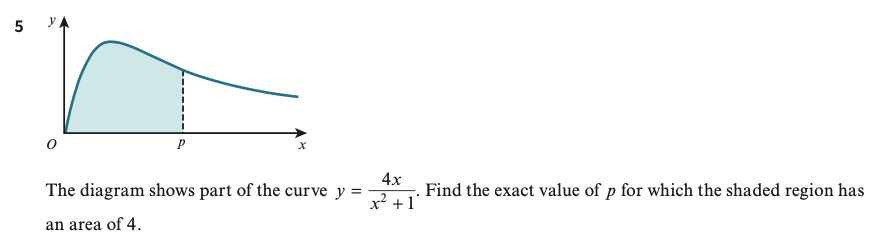
Answers

Integration by Substitution
This is a very powerful method to simplify an integration.
The integral and the limits must be changed to the new variable.
We must change back to the original variable at the end.
Worked Examples
1.) FInd the following indefinite integrals by making the suggested substitution. Remember to give your final answer in terms of x:
2.) Find the area of the shaded region for each of the following graphs:

3.) Use the substitution u = sinx + 1 to find
4.) Prove that
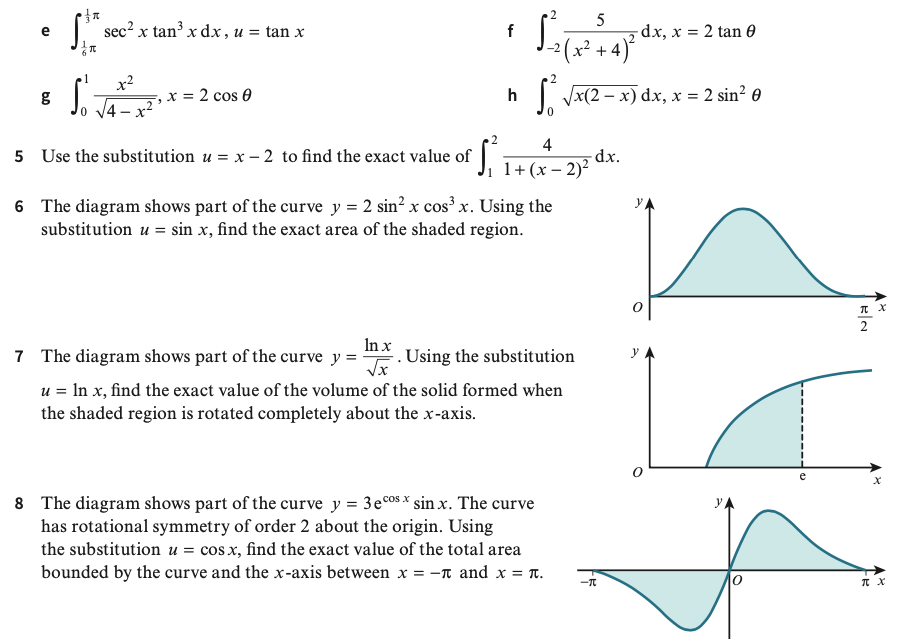
Exercise 4
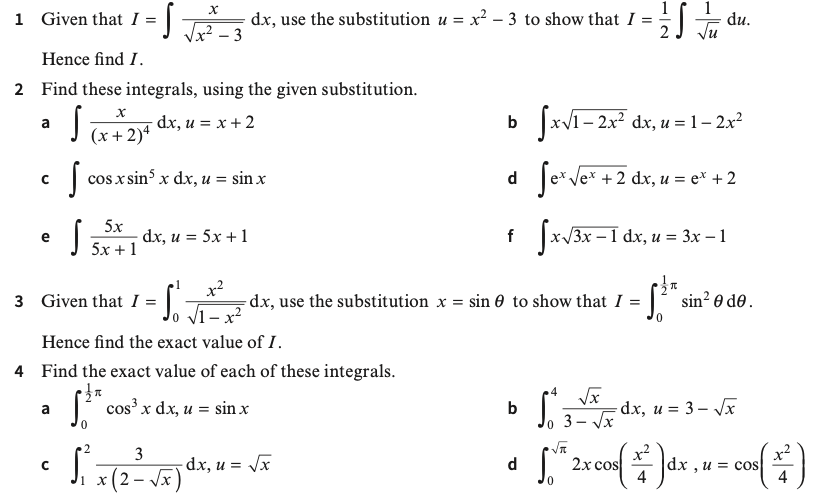
Answers
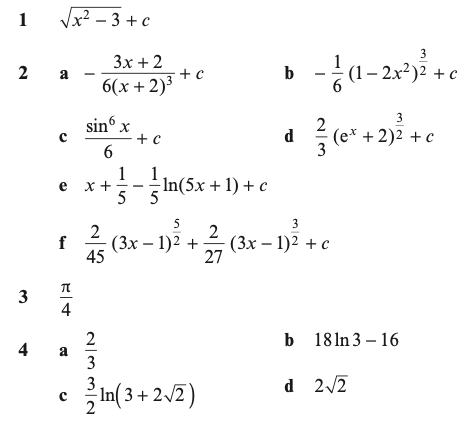
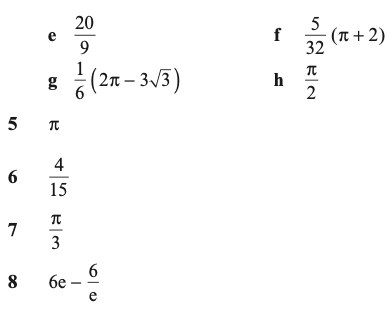
Using Partial Fractions in Integration
We can use partial fractions to make integration easier.
1.) Use partial fractions to find the following integrals:
Exercise 5

Answers
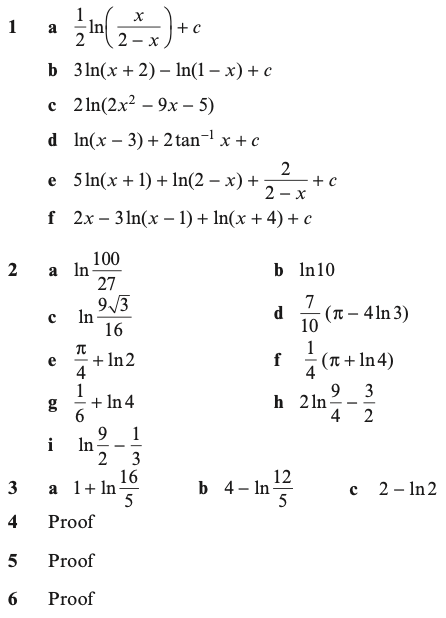
Integration by Parts
If an integral is a product of something easy to integrate and something difficult to integrate, we can use integration by parts to make it easier to integrate.
The integration by parts formula is derived by rearranging the product rule.
Integration by Parts Formula
Worked Examples
1.) Find
2.) Find
Sometimes we need to use the technique more than once.
3.) Find
Exercise 6
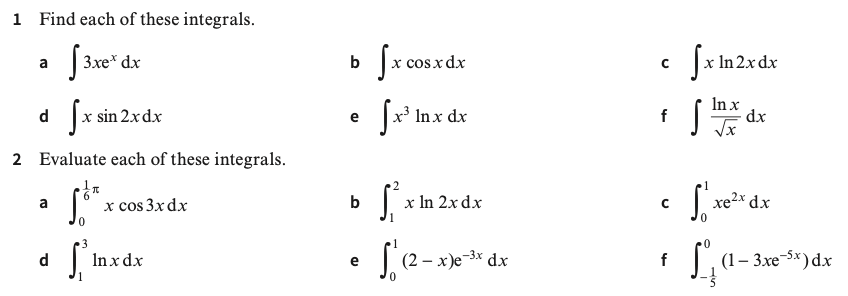
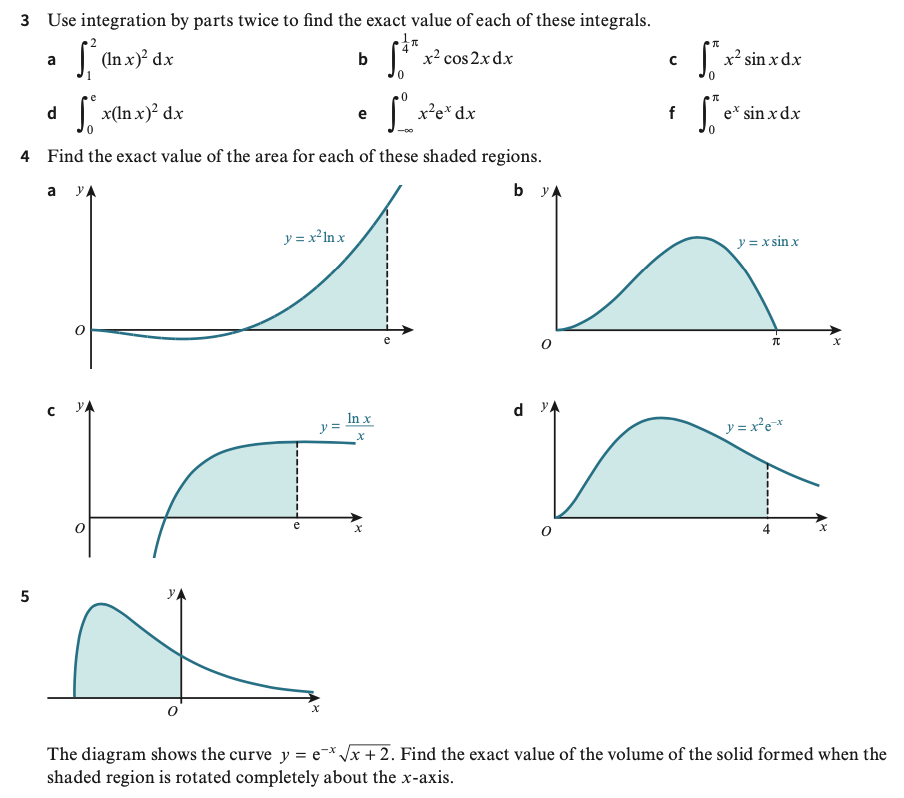
Mixed Exercise

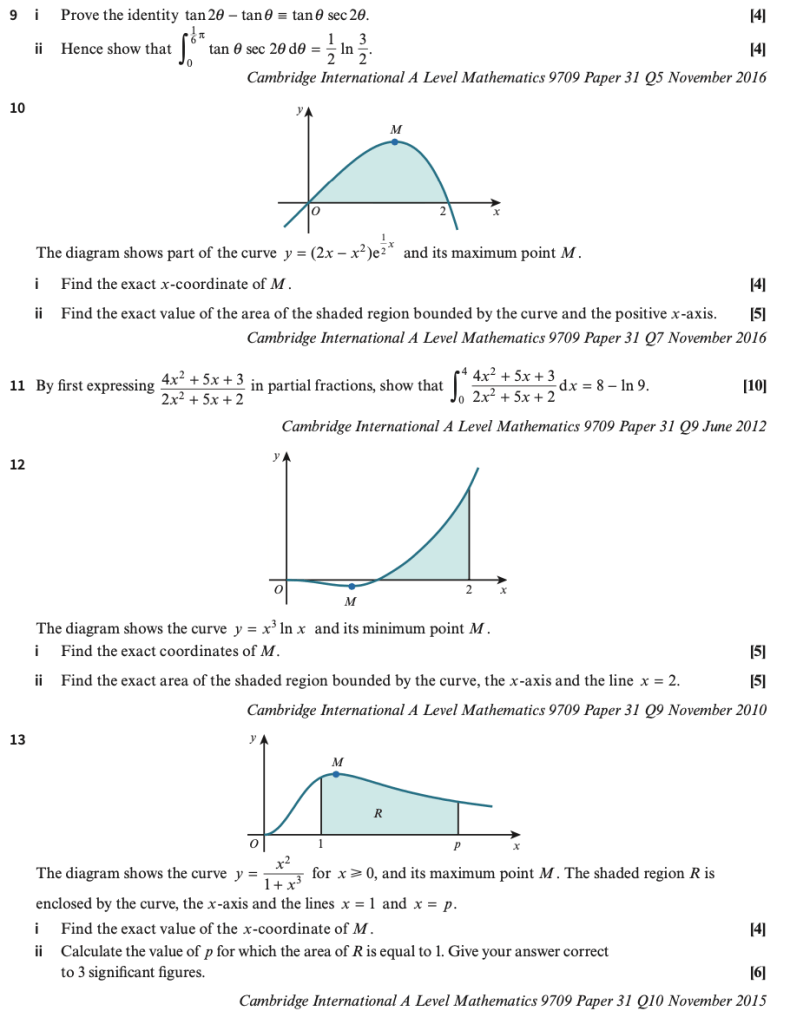
Answers
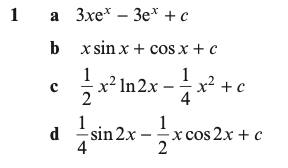

Mixed Exercise Answers