Maths with David

    9709. P3. Further Calculus. Past Exam Questions

    9709/31/M/J/25q4 – Mark Scheme

    The parametric equations of a curve are x = e^{tant} , y = 3 tan^2 t .

    Find the equation of the tangent to the curve at the point (e,3). Give your answer in the form y = mx + c , where m and c are exact. [6 marks]

    9709/31/M/J/25q11 – Mark Scheme

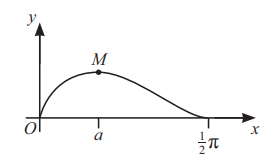
    The diagram shows the curve y = cosx \sqrt{sin 2x} for 0 \leq x \leq \frac{1}{2} \pi . The curve has a maximum point at M, where x = a.

    (a) Find the exact value of a [6 marks]

    (b) The region enclosed between the x-axis and the curve is rotated through 2 \pi radiancs about the x-axis. Find the exact volume of the solid generated. [5 marks]

    9709/32/M/J/25q10 – Mark Scheme

    (a) Find the quotient and remainder when x2 is divided by 1 +4x2. [2 marks]

    (b) Find the exact value of \int_0^{0.5} x tan^{-1} (2x) dx . [6 marks]

    9709/32/M/J/25q11 – Mark Scheme

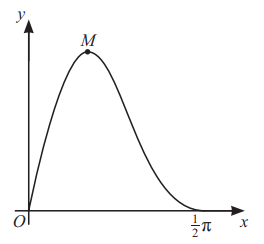
    The diagram shows the graph of y = 5sin2xcos2x for 0 \leq x \leq \frac{1}{2} \pi and its maximum point M.

    (a) Find the exact x-coordinate of M. [6 marks]

    (b) By using the substitution u = cos x, find the area of the region bounded by the curve, the x-axis between x = 0 and x = \frac{1}{4} \pi , and the line x = \frac{1}{4} \pi . [5 marks]

    9709/33/M/J/25q3 – Mark Scheme

    Find the exact value of \sum_{ \frac{1}{5} \pi }^ { \frac{1}{4} \pi } 3 cos^2 5x dx . [4 marks]

    9709/33/M/J/25q5 – Mark Scheme

    The equation of a curve is xy + y2e-x = 4

    (a) Show that \frac{dy}{dx} = \frac{ y^2 - ye^x }{ xe^x + 2y} [4 marks]

    (b) Find the gradients of the tangents to the curve when x = 0. [2 marks]