9709. P3. Differential Equations

What is a “Differential Equation”?

Types of Differential Equation

Ordinary vs. Partial

Linear vs. Non-linear

First order vs Second order

Solution of Differential Equations

General solution vs Particular solution

Initial conditions or Boundary conditions

Note: The solution to a differential equation is a function, not a value.

Separating variables technique

Developed by Johann Bernoulli (c. 1695)

Applies to any first order ODEs of the form: dy/dx =f(x).f(y)

Worked Examples

Find a general solution to the differential equation $(1+x^2) \frac{dy}{dx}=xtany$

2. Find the particular solution to the differential equation $\frac{dy}{dx} = \frac{-3(y-2)}{(2x+1)(x+2)}$ given that x=1 when y=4. Leave your answer in the form y=f(x).

Separating Variables Exercise 1

Answers

Exercise 1 Worked Solutions

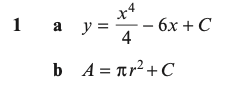
Solving Problems using ODEs

We need to get used to the language used in ODE questions. Whenever a rate is talked about, there is a change in a variable, so a derivative is needed. If it is not stated what it is changing over, then it is a change over time, i.e. dx/dt.

If y is proportional to x we write y=kx, if y is inversely proportional to x, we write y=k/x

Worked Examples

1.) The rate of increase of a population P of microorganisms at time t, in hours, is given by $\frac{dP}{dt}=3P, k>0$ . Initially the population size was 8.

Find a model for P in the form P=Ae^3t, stating the value of A;
Find, to the nearest hundred, the size of the population at time t=2;
Find the time at which the population will be 1000 times larger than its starting value;
State one limitation of this model for large values of t.

2.) Water is contained by a 20m diameter cylindrical tank. It flows from the bottom of the tank through a tap at a rate proportional to the cube root of the volume.

Show that t minutes after the tap is opened, $\frac{dh}{dt}=-k\sqrt[3]{h}$ for some constant k;
Show that the general solution to this differential equation may be written as h=(P-Qt)^3/2, where P and Q are constants;
Initially the height of the water is 27m. 10 minutes later the height is 8m.
- Find the values of the constants P and Q;
- Find the time in minutes when the water is at a depth of 1m.

3.) The acceleration of an object is inversely proportional to its velocity at any given time and the direction of motion is taken to be positive. When the velocity is 1ms^-1, the acceleration is 3ms^-2.

Find a differential equation to model this situation;
Find the particular solution to this differential equation for which the initial velocity is 2ms^-1;
In this case, how long does the object take to reach a velocity of 8ms^-1?

Exercise 2