Maths with David

    9709. P3. Complex Numbers

    Sets of Numbers

    What are the natural numbers? Why are they not sufficient?

    What are the integers? Why are they not sufficient?

    What are the rational numbers? Why are they not sufficient?

    What are the real numbers? Why are they not sufficient?

    Complex Numbers

    Any real multiple of the square root of minus one (e.g. √(-16)) is called an imaginary number.

    The sum of a real number and an imaginary number is called a complex number, denoted z=a+bi (a,b are real).

    The complex numbers form a 2-dimensional number system, where the real part (Re(z)) has a different dimension to the imaginary part (Im(z))

    We typically call complex numbers z or w.

    We can represent a complex number either as a point on the plane or as a vector in the plane.  The x-axis represents the real component and the y-axis represents the imaginary component.  In this context, the xy-plane is referred to as an Argand diagram.

    Worked Example

    1.) Solve the equation z2-6z+58=0 and check the roots.

    2.) The complex numbers z1 and z2 are given by: z1 = (3-a) + (2b-4)i and z2 = (7b-4) + (3a-2)i.

    • Given that z1 and z2 are equal, find the value of a and b.
    • Check your answer by substituting your values for a and b into the expressions above.

    Short Exercise

    1.)

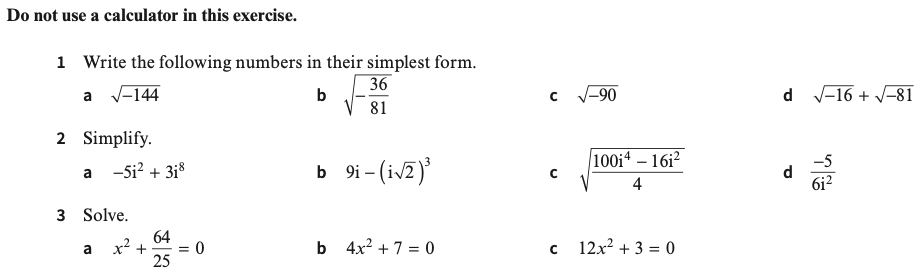
    Answers

    Short Exercise Worked Solutions

    Properties of Complex Numbers

    If Re(z)=0, number is completely imaginary, if Im(z)=0, number is completely real.

    If z=a+bi and w=c+di, then z=w <=> a=c and b=d

    If z=a+bi, then z*=a-bi is the complex conjugate of z, which has the special properties that:

    • z+z*=2a
    • z-z*=2bi
    • zz*=a2+b2

    Arithmetic with Complex Numbers

    Addition, subtraction and multiplication are obvious (although it is worth memorising how complex numbers combine in multiplication).

    Division is done using the “difference of two squares” formula.

    Worked Examples

    1.) Find real numbers p and q such that p+iq = \frac{1}{3+5i};

    2.) Find the real and imaginary parts of \frac{1}{5+2i};

    3.) Express \frac{9-4i}{2+3i} as a complex number in the form x+iy;

    Exercise 2

    Answers

    Exercise 2 Worked Solutions

    Geometric representation of complex numbers

    Same scale should be used on the real and imaginary axes of the Argand Diagram.

    A complex number can be represented by a point or by a vector.

    Once we have calculated the modulus and the argument, we may write the complex number in trigonometric form or in exponential form. Both are equivalent.

    This greatly simplifies arithmetic, as we now multiply by multiplying the moduli and adding the arguments and divide by dividing the moduli and subtracting the arguments.

    Polar Form

    Complex  numbers can be expressed in rectangular form or in polar form, where we specify the length and the angle.

    We calculate the modulus (i.e. the length) using Pythagoras’ theorem and the argument (i.e. the angle) by taking tan-1(b/a) and adding or subtracting π as necessary based on the quadrant it is in.

    Worked Examples

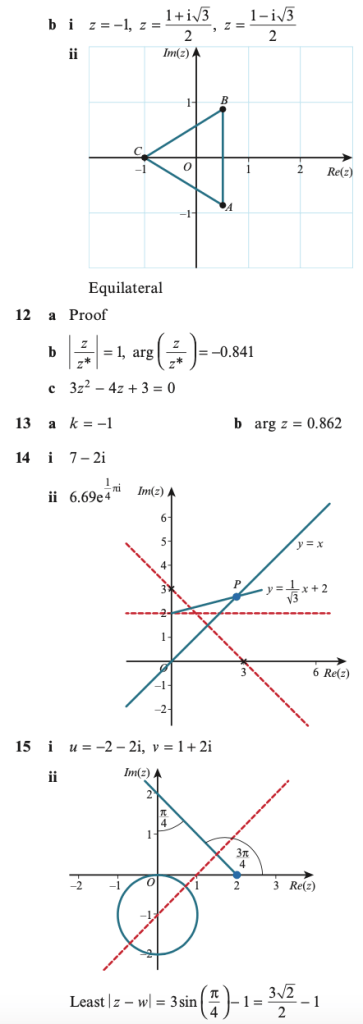
    1.) z = 2+5i and w = 4+2i. Show z, w and z-w on an Argand diagram.

    2.) Find (to 2 decimal places) the modulus and argument (in radians) of:

    • z = 2+7i;
    • z = -5+2i;
    • z = -4-i.

    3.) Express the numbers z1 = 1+i√3 and z2 = -3-3i in the from r(cos𝜽+isin𝜽). Also, write down the value of |z1z2|.

    4.) Write each of the following complex numbers in the form x+yi, giving surds in your answer where appropriate:

    • 6(cos(- \frac { \pi}{4}) + isin(- \frac { \pi}{4}))
    • 3(cos(- \frac { \pi}{6}) + isin(- \frac { \pi}{6}))

    Exercise 3

    Answers

    Exercise 3 Worked Solutions

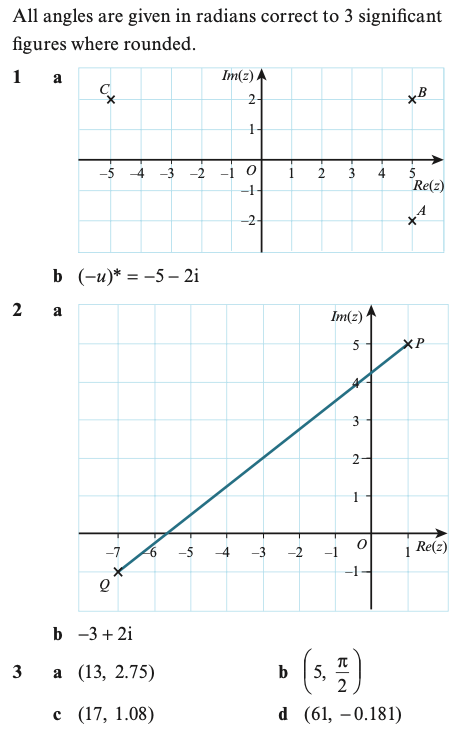
    Solving Equations

    A quadratic equation has two roots, x1 and x2.  

    If ∆>0 then x1 and x2 are distinct real numbers.

    If ∆=0 then x1 and x2 are the same real number.

    If ∆<0 then x1 and x2 are a conjugate pair of complex numbers

    Fundamental Theorem of Algebra

    A polynomial equation of degree n has n complex roots (proof is 3rd year university level).

    Cubic Equation

    A cubic equation can always be written as the product of a linear factor and a quadratic factor, so it always has at least one real root (the other two roots are either real or a complex conjugate pair).

    Quartic Equations

    A quartic equation has 4 roots, which may be:

    • 4 reals; or
    • 2 reals and a complex conjugate pair; or
    • 2 complex conjugate pairs.

    Square root of a complex number

    We can find the square root of a complex number a+bi by writing (c+di)2 and then calculating c and d.

    Advanced students may wish to derive a formula for this by following the process algebraically.

    If z3=1, then z3-1=0

    So z=1 is clearly a root, and dividing through by the factor z-1 finds us the other two complex roots.

    These roots can be used when solving a cubic equation, by rewriting it.  e.g. z3=8

    Worked Examples

    1.) Find the two square roots of 8+6i;

    2.) Given that 2i is a root of z4 + 13z2 + 36 = 0, find the other roots.

    3.) Show that z=4 is a root of the equation z3 – 3z2 – 3z – 4 = 0 and find all complex solutions of this equation.

    Exercise 4

    Answers

    Exercise 4 Worked Solutions

    Loci

    Just like an algebraic equation can be represented by a curve in the Cartesian plane, a complex equation is represented by a “locus” on an Argand diagram.  There are a few standard geometrical representations which we need to be aware of.

    Circles

    |z|=r is a circle of radius r centred at the origin.

    |z|< r is a disc of radius r (we use a dotted line if the inequality is strict and a solid line if not).

    |z-z1|=r is a circle of radius r centred at z1.

    We can convert between |z-z1|=r and (x-x1)2+(y-y1)2=r2, if it helps us to solve problems.

    Thinking in vector terms, let z be OP and z1 be OQ. Then z-z1= QP, so |z-z1|=r means that |QP|=r, which is a circle or length r centred at Q.

    Alternatively we can read |z-z1| as all points z at a fixed distance from z1. (i.e. absolute value of difference -> distance).

    Line Segments

    Instead of fixing a distance from a fixed point, we can fix an angle from a fixed point, allowing the distance to vary, which gives a half-line from that point:

    arg(z-z1)=ø

    If we are told that arg (z1-z)=µ, then the angle we need to measure from z1 is -(π-µ). (We can read it as saying that the argument from any point to our fixed point is fixed at angle µ).

    Perpendicular Bisectors

    |z-z1|=|z-z2| is the perpendicular bisector line between z1 and z2 (we can read it as saying “all points z whose distance from z1 is equal to their distance from z2”). 

    |z-z1|<|z-z2|is the half-plane extending from this perpendicular bisector.

    N.B. We can sketch the perpendicular bisector, or calculate it using normal coordinate geometry methods.

    Worked Examples

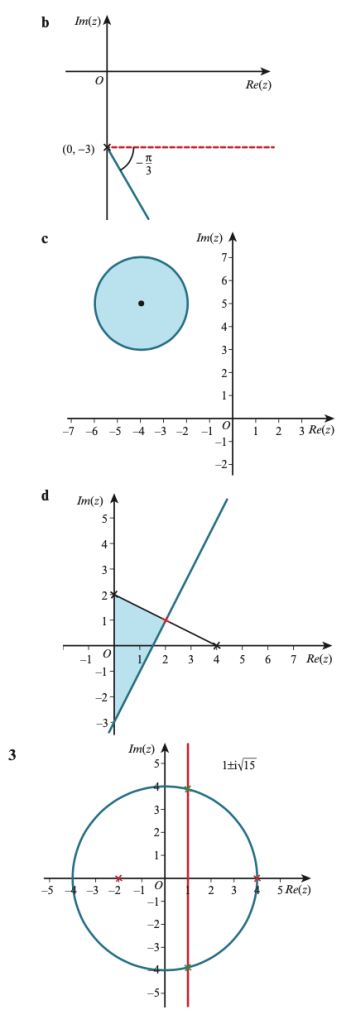
    1.) Draw Argand diagrams showing the set of points z for which:

    • arg z = π/4
    • arg (z-i) = π/4
    • 0 ≤ arg(z-i) ≤ π/4

    2.) On a simple Argand diagram sketch the loci |z| = 5 and |z-5|=|z|. Hence determine the complex numbers represented by points common to both loci.

    Exercise 5

    Mixed Exercise

    Exercise 5 Answers

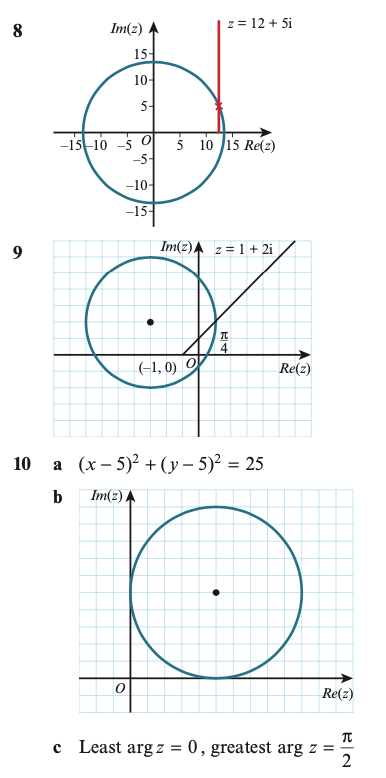
    Mixed Exercise Answers

    Exercise 5 & Mixed Exercise Worked Solutions