Modulus Function

In general, a modulus function is a function of the form y = |f(x)|.

When f(x) ≥ 0, then |f(x)| = f(x), however when f(x)<0, then |f(x)| = -f(x)

So what is the domain and range of |f(x)|?

Solving equations with modulus functions

Worked Examples

1. Solve the equation |2x-1| =5
2. Solve the equation |3x-5| = 2 – x/2

Graphs

To draw a graph of |f(x)| from a graph of f(x) we simply reflect all the parts below the x-axis in the x-axis.

For graphs with two moduli (i.e. f(x)=|x-3|+|1-x|), we need to separately consider the parts of the graph as individual cases (e.g. x<1, 1<x<3, x>3).

We will use this approach both for graphing and for solving such functions.

|a x b| = |a| x |b| and also || = (provided b is not zero).

Note that |b-a| is the distance between a and b.

If a>0, then |x-k|<a <=> k-a< x <k+a

Worked Examples

1. Sketch the graph of y = |3x-2|;
2. Rewrite |x+4| > 6 without a modulus sign;
3. Sketch the graph of y = |x-4| + |3x-1|.

(Please note that there are two exercises below – the first is practicing algebra and the second is practicing graphs. Below the exercises is a second section about inequalities)

Exercise 1

Answers to Exercise 1

Worked Solutions to Exercise 1

Exercise 2

Answers to Exercise 2

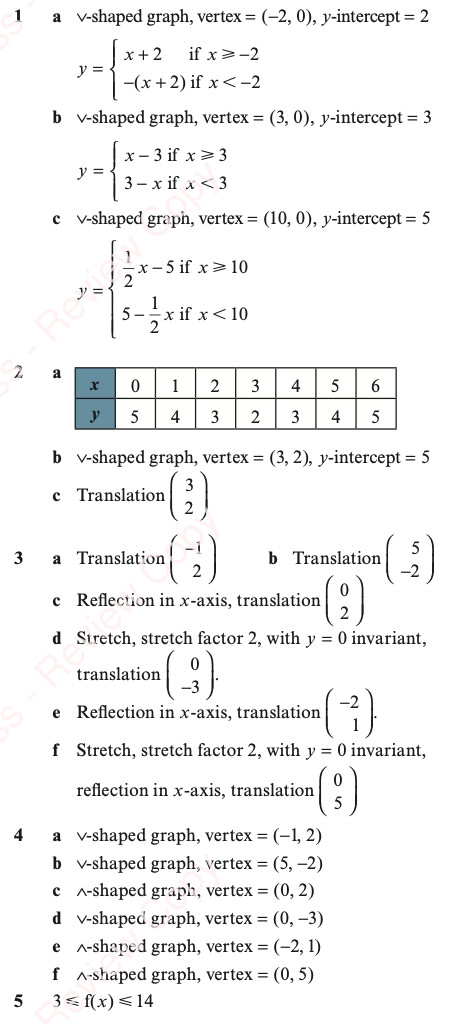
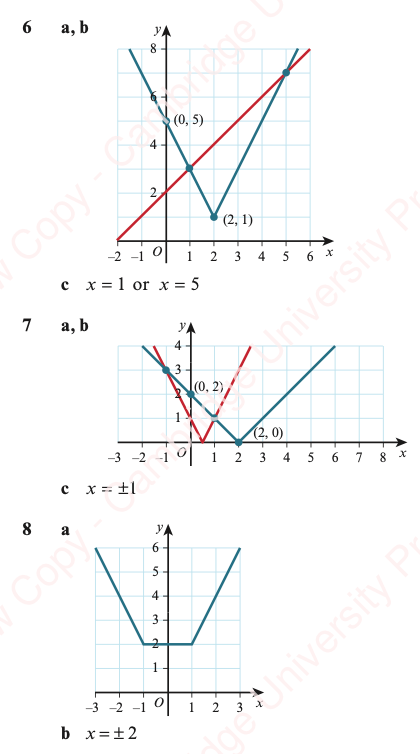
Worked Solutions to Exercise 2

Solving inequalities with modulus functions

Worked Examples

1. Solve |5x-1| > 3x;
2. Solve |2x-5| < 3;
3. Solve |2x-1| ≥ |3-x|.

Exercise 3

Answers to Exercise 3

Worked Solutions to Exercise 3