Maths with David

    9709. P1. Integration. Past Exam Questions

    November 2025 (9709/12). Question 5

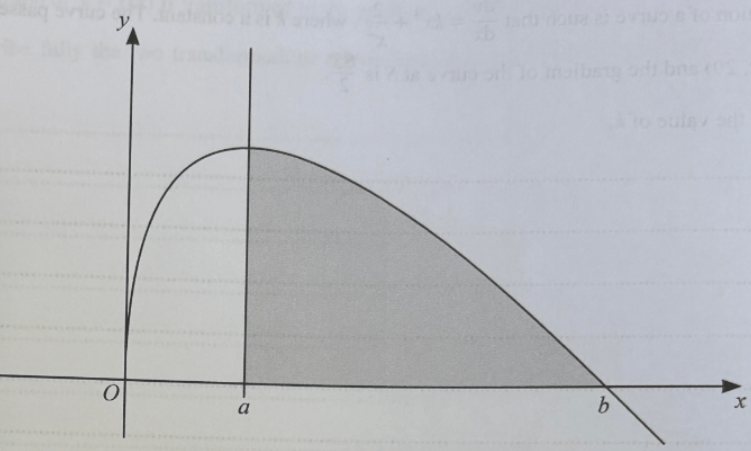
    The equation of the curve above is y = 4x ^ {1/2} - x . The curve has a maximum point when x = a and crosses the x-axis at the point with coordinate (b,0), where b > 0. The shaded region is bounded by the curve, the line x = a and the x-axis (see diagram).

    (a) Find the value of a. [3 marks]

    (b) Find the exact area of the shaded region. [5 marks].

    9709/11/M/J/25q4

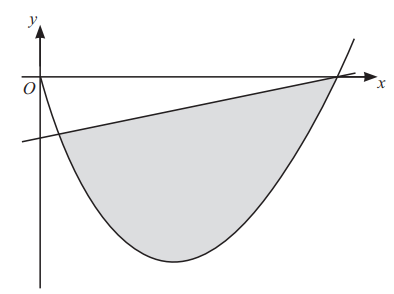
    The diagram shows the curve with equation y = 5x^{ \frac{3}{2} } - 20x and the line with equation y = x – 16. The x coordinates of the points of intersection of the curve and the line are 1 and 16.

    Find the area of the shaded region between the curve and the line. [5 marks]

    9709/11/M/J/25q2

    The equation of a curve is such that \frac{dy}{dx} = 4(2x-5)^3 - 9x^{ \frac{1}{2} } . The curve passes through the point A(4, - \frac{11}{2} ) .

    (a) Find the gradient of the normal to the curve at the point A. [2 marks]

    (b) Find the equation of the curve. [4 marks]

    9709/12/M/J/25q6

    The diagram shows the curve with equation y = \frac{9}{(5x+4)^{ \frac{1}{2}} } and the line y = 6 – 3x. The line and the curve intersect at the point P which has y-coordinate 3.

    Find the area of the shaded region. [6 marks]

    .