November 2025 (9709/12). Question 3

(a) The graph of y = f(x) is transformed to the graph of y = f(3x) + 2. Describe fully the two transformations which have been combined to give the resulting graph. [3 marks]

(b) A different graph has equation y = g(x). This graph is stretched by scale factor 3 in the y-direction and then reflected in the y-axis. Write down the equation of the transformed graph in terms of the function g. [2 marks]

9709/11/M/J/25q10 – Mark Scheme

The functions f and g are defined by:

for ,

for

(a) Describe fully a sequence of transformations which transforms the graph of y = f(x) to the graph of y = g(x). You should make clear the order in which the transformations are applied. [5 marks]

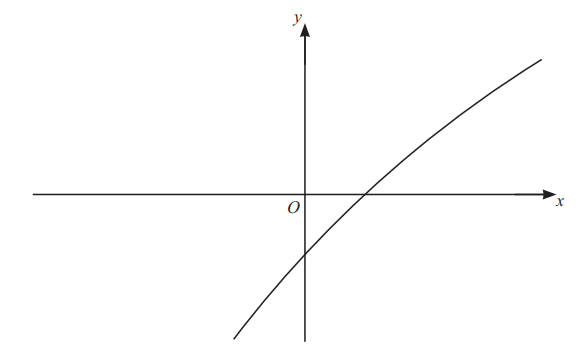
The diagram shows the graph of y = g(x).

(b) On the diagram sketch the graph y = g^-1(x) together with any relevant mirror line. [2 marks]

(c) Find an expression for g^-1(x). [2 marks]

(d) State the range of g^-1. [1 mark]

The function h is defined by h(x) = x-2 for .

(e) Find the value of g^-1h(4). [1 mark]

(f) Explain why the composite function hg-¹ cannot be formed. [1 mark]

9709/12/M/J/25q1

The diagram shows the graphs with equations y=f(x) and y=g(x).

Describe fully a sequence of two transformations which transforms the graph of y = f(x) to the graph of y = g(x). Make clear the order in which the transformations should be applied. [4 marks]