Kinematics is the study of motion.
Sometimes we will look at scalar quantities like distance and speed, and sometimes at vector quantities like displacement and velocity.
What is the difference between a scalar quantity and a vector quantity?
Speed and Distance
s = d ÷ t, where s = speed, d=distance covered and t = time taken. This applies for constant speed, or gives us the average speed if speed is not constant.
Similarly, average velocity = change in displacement ÷ time taken, which we can rearrange to write as s = v x t (s = displacement, v = velocity, t = time)
Clearly units should always be consistent. We will typically use SI units (distances in metres and time in seconds)
Models and Assumptions
When we make any assumptions (e.g that speed is constant), we should always consider whether the assumption is reasonable in the context of the question (and what the impact of changing the assumption would be).
Throughout this course we will be treating objects as particles that are not affected by things such as rotation or deformation.
Worked Examples
1.) A car travelling at constant speed travels 9km in 15 minutes. Find its speed in ms-1.
2.) A cyclist travels at 5ms-1 for 30s and then turns back and travels at 3ms-1 for 10s. Find her displacement in the original direction of motion from her starting position.
Exercise 1
1.) A cyclist covers 120m in 15s at constant speed. Find her speed.
2.) A sprinter runs at a constant speed of for 7s. Find the distance covered.
3a.) A cheetah spots a grazing gazelle 150m away and runs at a constant speed of to catch it. How long does it take the cheetah to catch it?
3b.) What assumptions have been made to answer this questions?
4.) The speed of light is , to 3 significant figures. The average distance between the Earth and the Sun is 150 million km (also to 3 significant figures). How long does it take for light from the Sun to reach the Earth (on average). Give your answer in minutes and seconds.
5.) The land speed record was set in 1997 as . Find how long in seconds it took to cover 1km when the record was set.
6a.) A runner runs at for 7s before increasing the pace to
for the next 13s. Find her average speed.
6b.) What assumptions have been made to answer this question?
7a.) A remote control car travels forward at in Drive and backwards at
in Reverse. The car travels for 10s in Drive before traveling for 5s in Reverse. Find its displacement from its starting point.
7b.) Find its average velocity in the direction in which it started driving forwards.
7c.) Find its average speed.
8.) A speed skater averages over the first 5s of a race. Find the average speed required over the next 10s to average
overall.
9.) The speed of sound in wood is and the speed of sound in air is
. A hammer hits one end of a 33m long plank of wood. Find the difference in time between the sound waves being detected at the end of the plank and the sound being heard through the air.
10.) An exercise routine involves a mixture of jogging at and sprinting at
. An athlete covers 1km in 3 minutes and 10 seconds. How long does she spend sprinting.
11.) Two cars are racing over the same distance. They start at the same time, but one finishes 8s before the other. The faster one averaged and the slower one averaged
. Find the length of the race.
12.) Two air hockey pucks are 2m apart. One is struck and moves directly towards the other at . The other is struck 0.2s later and moves directly towards the first at
. Find how far the first puck has moved when the collision occurs and how long it has been moving for.
Exercise 1 Answers
1.)
2.) 63m
3.a) 6s
3.b) The cheetah can instantly attain their top speed. The gazelle remains stationary.
4.) 8 minutes and 20 seconds
5.) 2.94s
6a.)
6b.) The speeds are average speeds or the runner instantaneously changes speed between sections.
7a.) 45m
7b.)
7c.)
8.
9. 0.09s
10. 80s
11. 15,840m
12. 1.014m in 0.78s
Acceleration
Acceleration is a vector quantity that measures the time taken of a change in velocity: ; u = initial velocity, v = final velocity.
Positive acceleration represents an increase in velocity over time and negative acceleration reflects a decrease in velocity over time.
If acceleration is constant, then average velocity = and so displacement is
Worked Examples
- A parachutist takes 5 seconds to fall from rest to 49ms-1. What is her acceleration?
- A tractor accelerates from 5ms-1 to 9ms-1 at 0.5ms-2. Find the distance covered by the tractor during this period.
- A cyclist is travelling along a straight road. He accelerates at a constant rate from a speed of 4ms-1 to a speed of 7.5ms-1 in 40s. Find:
- the distance that he travels in these 40 seconds; and
- his acceleration in these 40 seconds.
Exercise 2
1.) A car accelerates from to
in 3s at constant acceleration. Find its acceleration.
2.) A car accelerates from rest to in 4s at constant acceleration. Find its acceleration.
3.) A car accelerates from at an acceleration of
. Find the time take to reach
4.) An aeroplane accelerates at a constant rate of for 5s from an initial velocity of
. Find its final velocity.
5.) A speedboat accelerates at a constant rate of for 4s, reaching a final velocity of
. Find its initial velocity.
6.) A car decelerates at a constant rate of for 3s, finishing at a velocity of
. Find its initial velocity.
7.) A car accelerates from an initial velocity of to a final velocity of
at a constant rate of
. Find the car’s displacement in that time.
8a.) A sprinter covered 60m in 10s accelerating from a jog. Her final velocity is . Calculate here acceleration.
8b.) What assumptions have been made to answer this question?
9.) A wagon is accelerating down a hill at constant acceleration. It took 1s more to accelerate from a velocity of to a velocity of
than it took to accelerate from rest to a velocity of
. Find the acceleration.
10.) A driver sees a junction 100m ahead. She lets her car slow at constant deceleration of and arrives at the junction 10s later. Find the velocity she is travelling when she reaches the junction.
11.) A cyclist is travelling at a velocity of when he reaches the top of a slope, which is 80m long. There is a bend at the bottom of the slope, which would be dangerous to go round at any faster than
. Because of gravity, if he did not pedal or brake, he would accelerate down the slope at
. To go as fast as possible, but still reach the bottom at a safe speed, should the cyclist brake, do nothing, or pedal?
Exercise 2 Answers
1.)
2.)
3.) 1.5s
4.)
5.)
6.)
7.) 48m
8a.)
8b.) The sprinter can maintain a constant acceleration and we are ignoring the shape of the sprinter’s body and the different positions it takes when running, by considering the sprinter having a single position at any point in time.
9.)
10.)
11.) He can pedal because doing nothing he will arrive at the bend with velocity .
Constant Acceleration Formuale
(1.)
(2.)
(3.)
(4.)
(5.)
You should memorise these formulae. which are the most important in mechanics. The first two have been mentioned above and the remaining three you will derive in a following exercise
Worked Examples




Exercise 3
1.) For each part of question 1, assume constant acceleration, write down the equation relating the four variables in the question, and use it to find the missing variable:
1a.) Find s when ,
and t=4s
1b.) Find s when ,
and t=8s
1c.) Find a when s=40m, and t=5s
1d.) Find a when s=28m, and t=4s
1e.) Find a when s=24m, and
1f.) Find u when s=45m, and t=6s
1g.) Find v when s=24m, and t=4s
1h.) Find s when ,
and
2.) For each part of question 2, assume constant acceleration and find the first time t, for positive t, when the following situations occur:
2a.) Find t when ,
and s=24m
2b.) Find t when ,
and s=21m
2c.) Find t when ,
and s=20m
3.) Assuming constant acceleration, find v when s=6m, and
if the object has changed direction during the motion.
4.) Assuming constant acceleration, find u when s = 60m, and
if the object has not changed direction during the motion.
5a.) Assuming constant acceleration, find v when s=18m, and
5
5b.) Why is it not necessary to specify in this question whether the object has changed direction during the motion?
6.) A car is travelling at a velocity of when the driver sees the traffic lights ahead change to red. He decelerates at a constant rate of
and comes to stop at the lights. Find how far away from the lights the driver started braking.
7.) An aeroplane accelerates at a constant rate along a runway from rest until taking off at a velocity of . The runway is 400m long. Find the acceleration of the aeroplane.
8.) An aeroplane accelerates from rest along a runway at a constant rate of . It needs to reach a velocity of
to take off. Find how long the runway needs to be.
9.) A motorcyclist sees that the traffic lights are red 40m ahead of her. She is travelling at a velocity of and comes to rest at the lights. Find the deceleration she experiences, assuming that it is constant.
10a.) A driver sees the traffic lights change to red 240m away when he is travelling at velocity of . To avoid wasting fuel, he does not brake, but lets the car slow down naturally. The traffic lights change to green after 12s, at the same time as the driver arrives at the lights. Find the speed at which the driver goes past the lights.
10b.) What assumptions have been made to answer the question?
11.) In a game of curling, competitors slide stones over the ice at a target 38m away. The stone is released directly towards the target with velocity and decelerates at a constant rate of
. Find how far from the target the stone comes to rest.
12.) A golf ball is struck 10m from a hole and is rolling towards the hole. It has an initial velocity of when struck and decelerates at a constant rate of
. Does the ball reach the hole?
13.) A driverless car registers the traffic lights change to amber 40m ahead. The amber light serves as a 2s warning before a red light. The car is travelling at and can accelerate at
or brake safely at
. What options does the car have?
14a.) You can use the first two SUVAT equations, i.e. v=u+at and to derive the other equations. By substituting for v in the second equation, derive
14b.) Derive the remaining two equations, and
from the original two equations.
15.) Show that an object accelerating with acceleration a from velocity u to velocity v, where 0<u<v, over a time t is travelling at a velocity of at time
, that is, that at the time halfway through the motion the velocity of the object is the mean of the initial and final velocities.
16.) Show that an object accelerating with acceleration a from velocity u to velocity v, where 0<u<v, over a displacement s is travelling at a speed of at a distance
. Hence, prove that when the object does not change direction the speed at the midpoint of the distance is always greater than the mean of the initial and final speeds. Deduce also that the mean of the initial and final speeds occurs at a point closer to the start of the motion than the end.
Answers

Displacement-Time Graphs and Multi-Stage Problems
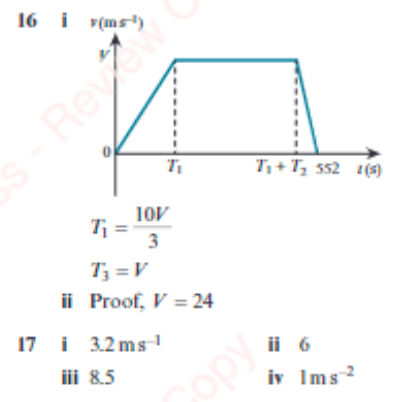
On graphs, time is always plotted on the x-axis.
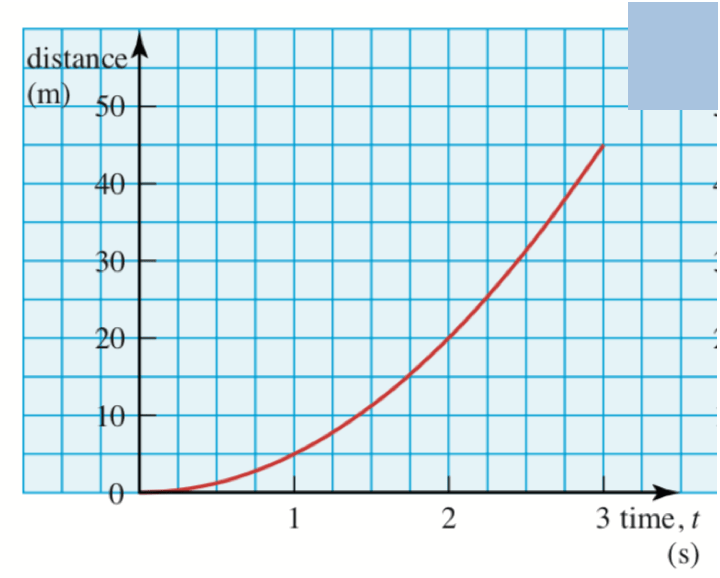
On a displacement-time (“s-t”) graph, a horizontal line indicates no movement. In general, the gradient of the line indicates the speed. A curve indicates that there is acceleration. The graph may go below the axis to indicate the opposite direction of motion.
Worked Examples
WE1.

WE2.
A sprinter in a 100 metre race pushes off the starting block with a speed of and accelerates at a constant rate. She attains her maximum speed of
after 40 metres and then continues at that speed for the rest of the race.
What is her time for the whole race?
Exercise



Answers


Velocity-time graphs, Speed-time graphs and Distance-time graphs

By contrast, on a velocity-time (“v-t”) graph, a horizontal line indicates constant speed. The gradient of a velocity-time graph indicates acceleration (think about the formula ). The area below the x-axis indicates negative velocity, which means the direction has changed.
Important: The area under a velocity time graph equals displacement.
Discontinuities
Sometimes velocity can appear to change instantaneously, for instance when a bat hits a ball. This will be represented on a v-t graph by a discontinuity. We can use a dotted line to mark this.
An s-t graph cannot have a discontinuity (until teleporting is invented 🤔), a bat hitting a ball would be represented by a sharp change in gradient, so the curve would not be smooth.
Worked Examples
WE1.
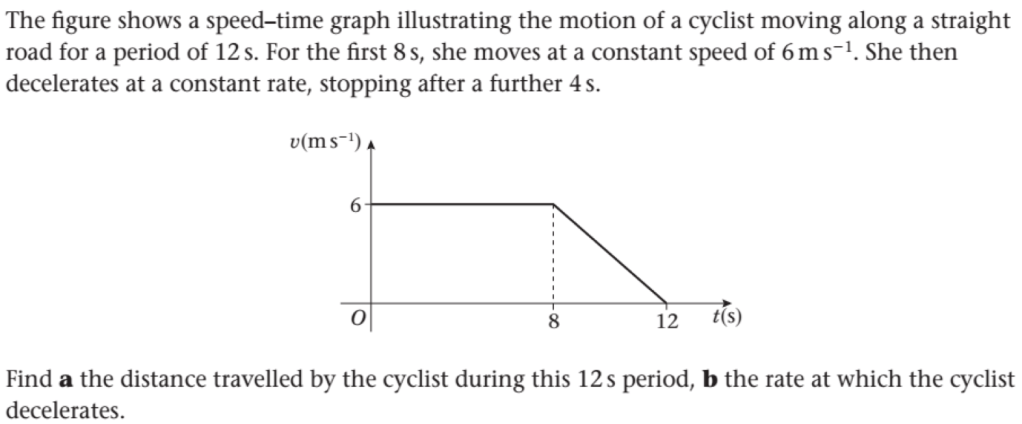
WE2.
A particle is moving in a straight line. The particle starts with speed and accelerates at a constant rate of
for 8 seconds. It then decelerates at a constant rate coming to rest in a further 12 seconds.
(a.) Sketch a speed-time graph illustrating the motion of the particle;
(b.) Find the total distance moved by the particle during its 20 seconds of motion;
(c.) Sketch a distance-time graph illustrating the motion of the particle.
WE3.

Various Exercises including Combined on Everything Above







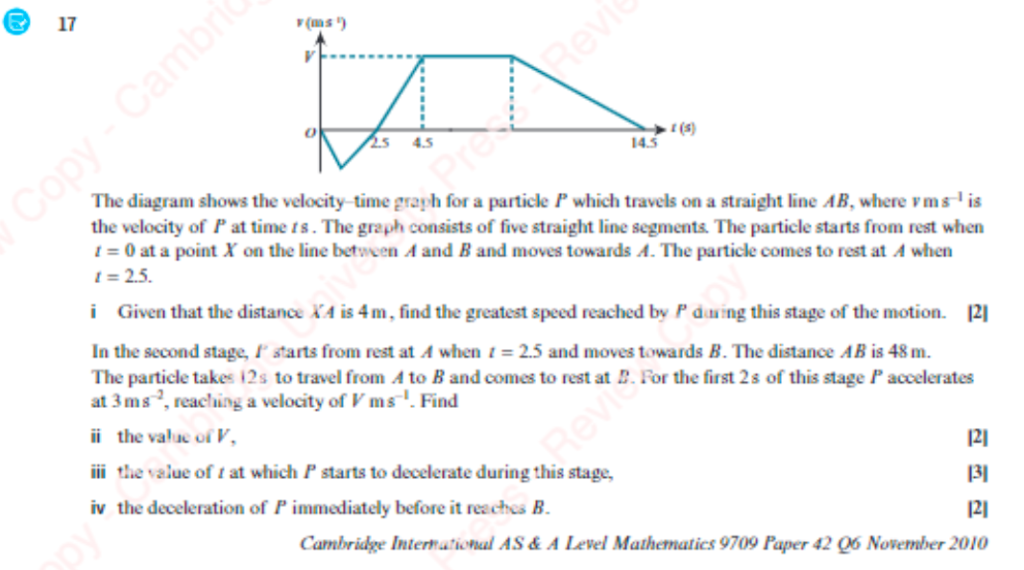
Answers




7.) 4s – Assumptions: e.g. Ball immediately starts moving at 4ms-1, acts as a particle, rebounds with same deceleration.

15. (i.) 0.02ms-2, -0.21ms-2, (ii) 42.5m, (iii) 86.5m