9709. Mechanics 1. Connected Particles

Past Paper Practice (Question from Summer 2017 paper 1)

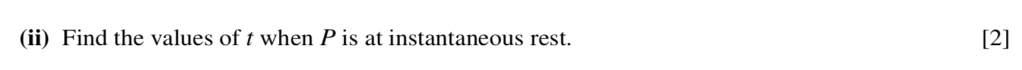
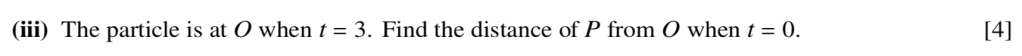
Mark Scheme

Newton’s third law: Theory

Newton’s Words: Actioni contrariam semper et æqualem esse reactionem: sive corporum duorum actiones in se mutuo semper esse æquales et in partes contrarias dirigi

Translated: To every action there is always opposed an equal reaction: or the mutual actions of two bodies upon each other are always equal, and directed to contrary parts

In modern terms: If an object exerts a force on another object, the second object exerts a force of equal magnitude in the opposite direction

Possible connectors and their natures (part 1):

Rod – rigid connector with no mass. If pulled can have a tension force inwards. If compressed can have a thrust force outwards.

Worked Examples

A car of mass 1500kg is towing a caravan of 500kg along a straight horizontal road. The resistance to motion is 80N on the car and 20N on the caravan. The driving force produced by the engine of the car is 360N. Find the tension in the tow bar.

A car tows a trailer along a straight horizontal road. The car has mass 1500kg and the trailer has mass 500kg. The resistance to motion is 80N on the car and 20N on the trailer. The driver applies the brakes, so the driving force is replaced by a braking force of 100N opposing the forward motion.
- Find the force in the tow bar.
- The car then descends a hill at 3º to the horizontal. The resistances and braking forces are unchanged. Find the new force in the tow bar.

A train comprises and engine and four trucks. The coupling between each is modelled as a rigid rod. The train moves along a straight horizontal track. The engine has a mass of 800g and each truck has a mass when empty of 200g. The resistance to motion is 0.06N on the engine and 0.01N on each truck. The engine produces a driving force of 3N.
- A mass of 100g is placed in each truck. Find the tension in each coupling.
- Find the tension in each coupling if, instead, the 400g is all placed in the last truck.

Exercise

Answers

Worked solutions

Strings and Pulleys: Theory

Possible connectors and their natures (part 2):

String – non-rigid connector with no mass. If pulled can have a tension force inwards. It cannot be compressed and cannot have a thrust force outwards.

A string exerts forces of equal magnitude on the objects attached to its two ends. If a string passes around a smooth pulley, the tension is unchanged

Worked Examples

Particles P and Q, of masses 2m and 3m, are attached to the ends of a light inextensible string. The string passes over a small smooth fixed pulley and the masses hang with the string taut. The system is released from rest:
- Find the acceleration of each mass;
- Comment on any modelling assumptions;
- Find the tension in the string;
- Find the distance moved by Q in the first 4 seconds, assuming that P does not reach the pulley.
Two particles A and B of masses 400g and 800g respectively are connected by a light inextensible string. Particle A lies on a rough horizontal table 4.5m from a small smooth pulley which is fixed at the edge of the table. The string passes over the pulley and B hangs freely, with the string taut, 50cm above horizontal ground. The coefficient of friction between A and the table is 0.2. The system is released from rest. Find:
- The acceleration of the system;
- The time taken for B to reach the ground;
- The total distance travelled by A before it first comes to rest.
A box of mass 3kg is placed on a table. The coefficient of friction between the box and the table is 0.5. A string is attached to the box and passes over a smooth pulley at the end of the table. The part of the string between the box and the pulley is horizontal. After passing over the pulley, the string hangs vertically, with the other end attached to a ball of mass 2kg. The system is released from rest.
- Find the tension in the string;
- The ball is initially 8cm below the table top. The ball hits the ground after 1.2s. The box has not reached the pulley by this time. Find the height of the table.
A crate of mass 500kg rests on a slope and is attached to a rope that passes over a smooth pulley. The slope is inclined at 20º to the horizontal. The coefficient of friction between the slope and the crate is 0.1. What happens to the crate when a force of 2000N is applied to the vertical part of the rope?

Exercise

Answers

Worked solutions

Internal and external forces

We can derive equations either from the system as a whole, ignoring internal forces, or from individual components of the system, using internal and external forces in the calculation

Objects moving up and down in lifts

If there is a person in a lift, we can consider the forces acting on the system as a whole, or just on the person or just on the lift, as indicated below. Note that if the lift is accelerating then the reaction force from the lift floor on the person will not be equal to the weight of the person.

Worked examples

A woman of mass 50kg is travelling in a lift of mass 450kg. The tension in the cable pulling the lift upwards is 5250N. Calculate the acceleration of the lift.
A man of mass 80kg and a woman of mass 70kg are travelling in a lift of mass 500kg. The tension in the cable pulling the lift upwards is 6890N. Calculate the acceleration of the lift and the reaction forces between the lift floor and each of the passengers.

Exercise and General Exercises